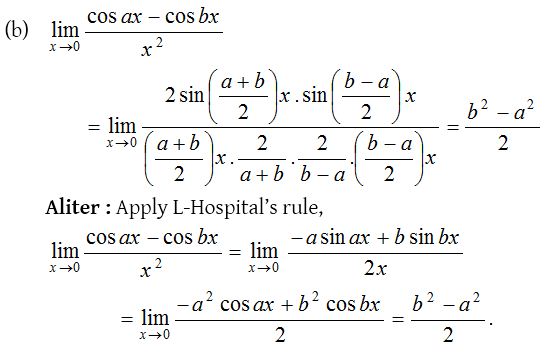Evaluating Limits
Methods of evaluation of limits
We shall divide the problems of evaluation of limits in five categories.
(1) Algebraic limits:
Let f(x) be an algebraic function and ‘a’ be a real number. Then ![]() is known as an algebraic limit.
is known as an algebraic limit.
- Direct substitution method: If by direct substitution of the point in the given expression we get a finite number, then the number obtained is the limit of the given expression.
- Factorisation method: In this method, numerator and denominator are factorised. The common factors are cancelled and the rest outputs the results.
- Rationalisation method: Rationalisation is followed when we have fractional powers (like etc.) on expressions in numerator or denominator or in both. After rationalisation the terms are factorised which on cancellation gives the result.
- Based on the form when x → ∞: In this case expression should be expressed as a function 1/x and then after removing indeterminate form, (if it is there) replace 1/x by 0.
(2) Trigonometric limits:
To evaluate trigonometric limit the following results are very important.
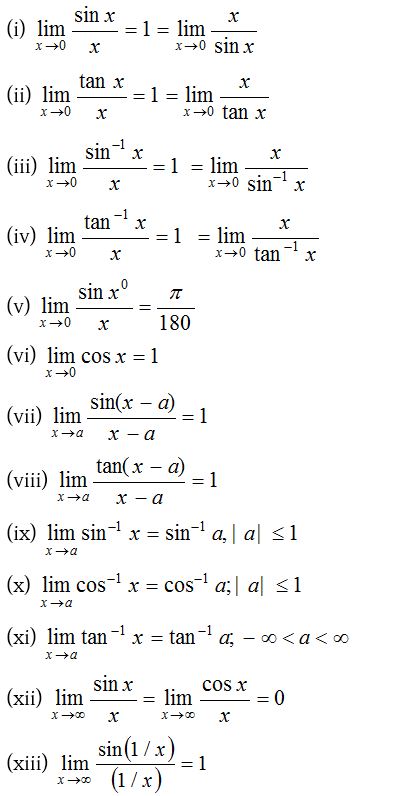
(3) Logarithmic limits:
To evaluate the logarithmic limits we use following formulae:
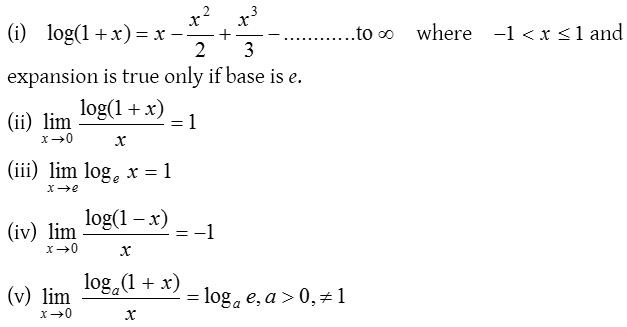
(4) Exponential limits:
(i) Based on series expansion:
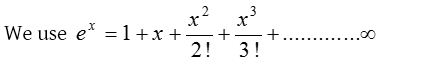
To evaluate the exponential limits we use the following results:
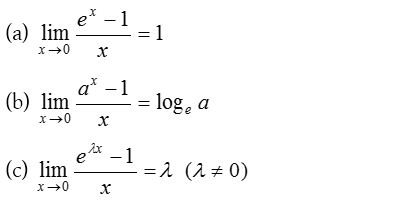
(ii) Based on the form 1∞: To evaluate the exponential form 1∞ we use the following results.
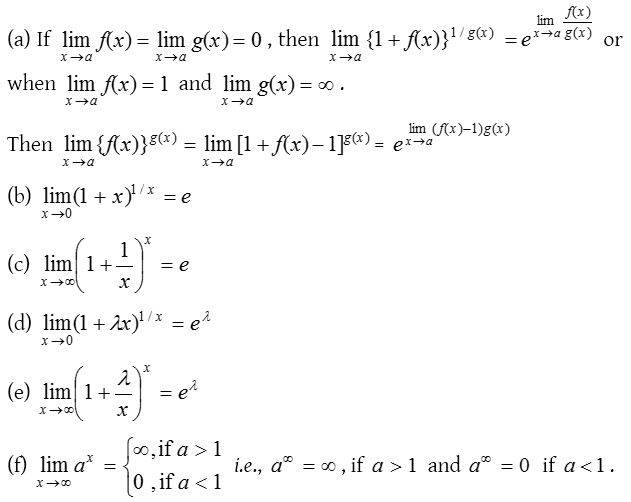
(5) L-Hospital’s rule:
If f(x) and g(x) be two functions of x such that

Sometimes it may be necessary to repeat this process a number of times till our goal of evaluating limit is achieved.
Evaluating Limits Problems with Solutions
1.
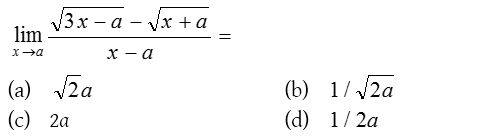
Solution:
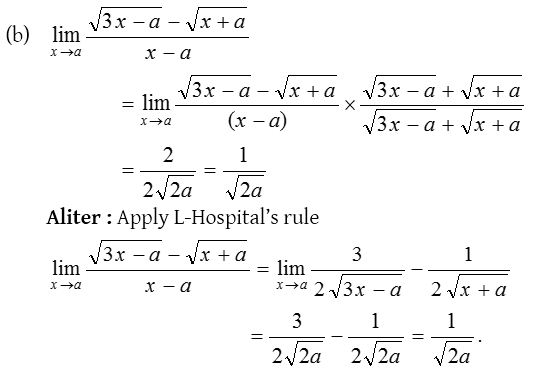
2.
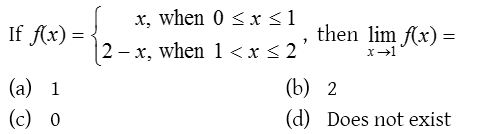
Solution:
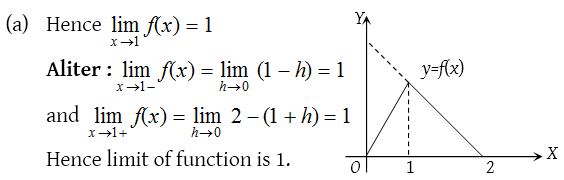
3.

Solution:
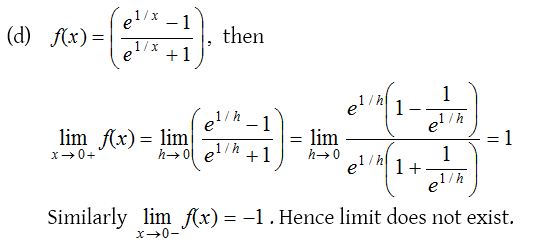
4.

Solution:
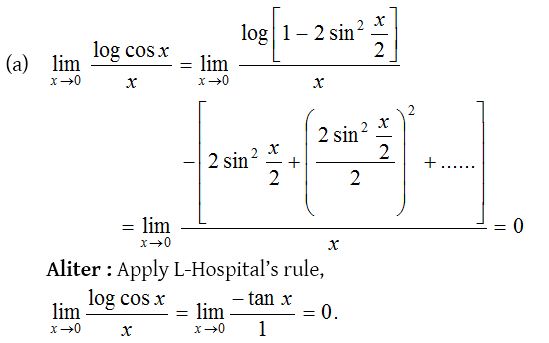
5.

Solution:
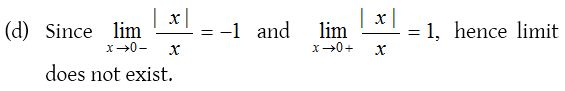
6.
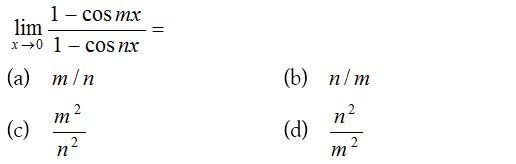
Solution:
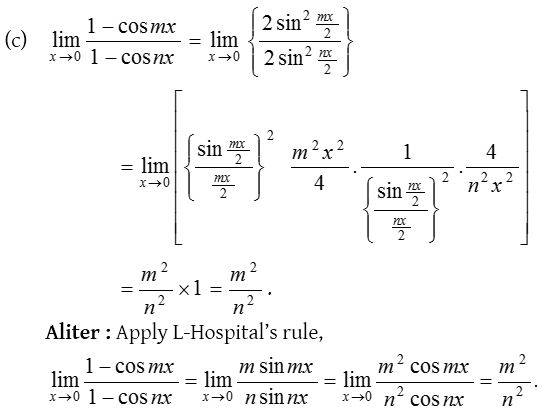
7.

Solution:
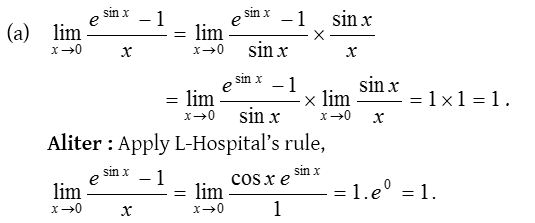
8.
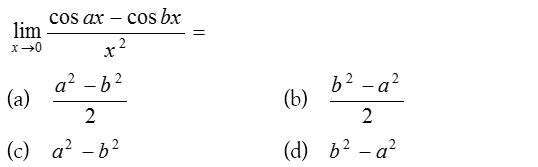
Solution: