Error in Differing Dimensions
Error increases when dimensions increase.
Consider the following example:
1. A student measures the side of a cube and accidentally reads a length of 5 inches, when the real length is 6 inches. Notice how the percentage of error increases as the student uses this measurement to compute surface area and volume.
 2. A box has the measurements 1.4 cm by 8.2 cm by 12.5 cm. Find the percent of error in calculating its volume.
2. A box has the measurements 1.4 cm by 8.2 cm by 12.5 cm. Find the percent of error in calculating its volume.
Answer: Since no other values are given, we will use the greatest possible error based upon the fact that these measurements were taken to the nearest tenth of a centimeter, which will be 0.05 cm.
Volume as measured: 1.4 × 8.2 × 12.5 = 143.5 cubic cm
Ma×imum volume (+0.05) : 1.45 × 8.25 × 12.55 = 150.129375 cubic cm
Minimum volume (-0.05): 1.35 × 8.15 × 12.45 = 136.981125 cubic cm
Possible error in volume: Maximum – measured = 6.629375 cubic cm
Measured – minimum = 6.518875 cubic cm
Use the “greatest” possible error in volume: 6.629375 cubic cm
Remember that percent of error is the relative error times 100%.
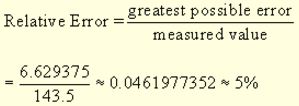
The percent of error is approximately 5%.
