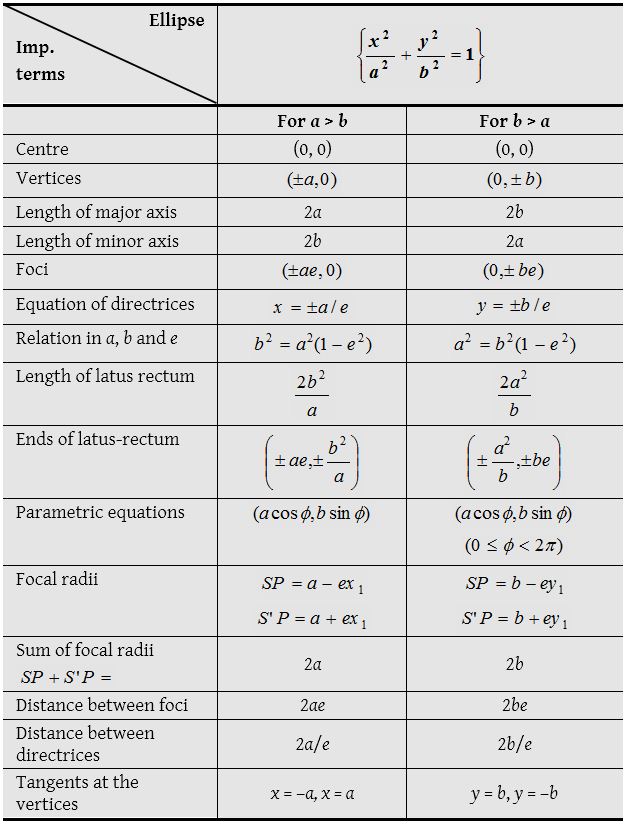
Ellipse
An ellipse is the locus of a point which moves in such a way that its distance from a fixed point is in constant ratio (<1) to its distance from a fixed line. The fixed point is called the focus and fixed line is called the directrix and the constant ratio is called the eccentricity of the ellipse, denoted by (e).
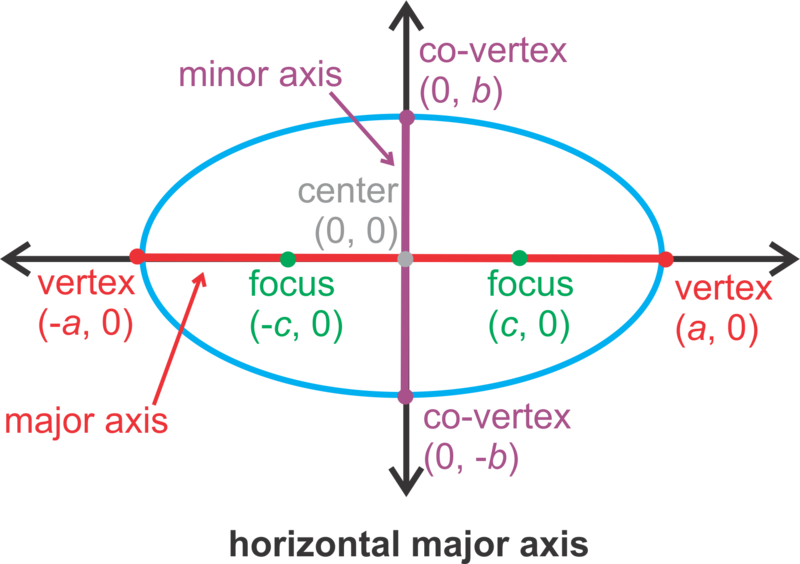
Standard equation of the ellipse
Let S be the focus, ZM be the directrix of the ellipse and P(x, y) is any point on the ellipse, then by definition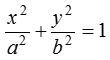 
, where b2 = a2(1 – e2).
Since e < 1, therefore a2(1 – e2) < a2 ⇒ b2 < a2.
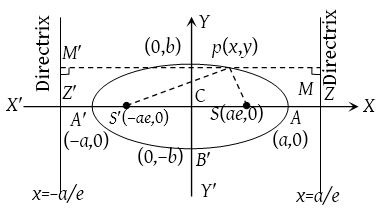The other form of equation of ellipse is 
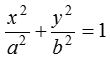, where, a2 = b2(1 – e2) i.e., a < b.
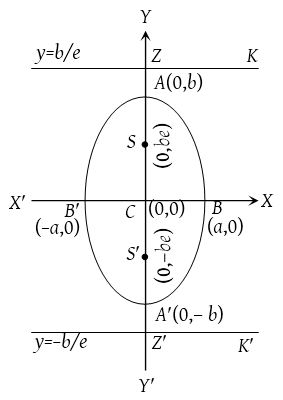Difference between both ellipses will be clear from the following table:
Parametric form of the ellipse
Let the equation of ellipse in standard form will be given by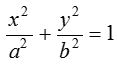 
.
Then the equation of ellipse in the parametric form will be given by x = a cos ϕ, y = b sin ϕ, where ϕ is the eccentric angle whose value vary from 0 ≤ ϕ < 2π. Therefore coordinate of any point P on the ellipse will be given by (a cos ϕ, b sin ϕ).
Special forms of an ellipse
(1) If the centre of the ellipse is at point and the directions of the axes are parallel to the coordinate axes, then its equation is
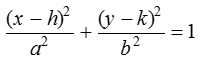
Position of a point with respect to an ellipse
Intersection of a line and an ellipse
The line y = mx + c intersects the ellipse 
in two distinct points if a2m2 + b2 > c2, in one point if c2 = a2m2 + b2 and does not intersect if a2m2 + b2 < c2.
Equations of tangent in different forms
