Direct Variation
- When two variable quantities have a constant (unchanged) ratio, their relationship is called a direct variation.
It is said that one variable “varies directly” as the other. - The constant ratio is called the constant of variation.
- The formula for direct variation is y = kx,
where k is the constant of variation.
“y varies directly as x”
(y = numerator; x = denominator)
In a direct variation, the two variables change in the same sense. If one increases, so does the other.
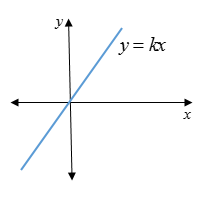
Graphically, direct variation y = kx when k > 0.
As x increases, y increases.
Example: The weekly salary a woman earns, S, varies directly as the number of hours, h, which she works. Express this relation as a formula.
Answer:
S varies directly with h
\(\frac { y }{ x } \) = k
⇒ \(\frac { S }{ h } \) = k
⇒ S = hk
