Dilations

Dilations

A dilation is a transformation (notation D_k) that produces an image that is the same shape as the original, but is a different size. A dilation stretches or shrinks the original figure.
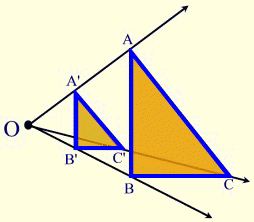The description of a dilation includes the scale factor (or ratio) and the center of the dilation. The center of dilation is a fixed point in the plane about which all points are expanded or contracted. It is the only invariant point under a dilation.

A dilation of scalar factor k whose center of dilation is the origin may be written: D_k(x, y) = (kx, ky).
If the scale factor, k, is greater than 1, the image is an enlargement (a stretch).
If the scale factor is between 0 and 1, the image is a reduction (a shrink).
(It is possible, but not usual, that the scale factor is 1, thus creating congruent figures.)

Properties preserved (invariant) under a dilation:

1. angle measures (remain the same)
2. parallelism (parallel lines remain parallel)
   
3. colinearity (points stay on the same lines)
4. midpoint (midpoints remain the same in each figure)
5. orientation (lettering order remains the same)
6. distance is NOT preserved (NOT an isometry)
   (lengths of segments are NOT the same in all cases except a scale factor or 1.)

Dilations create similar figures.

Definition: A dilation is a transformation of the plane, D_k, such that if O is a fixed point, k is a non-zero real number, and P’ is the image of point P, then O, P and P’ are collinear and \(\frac { O{ P }^{ ‘ } }{ OP } =k\).
Notation: D_k(x, y) = (kx, ky)
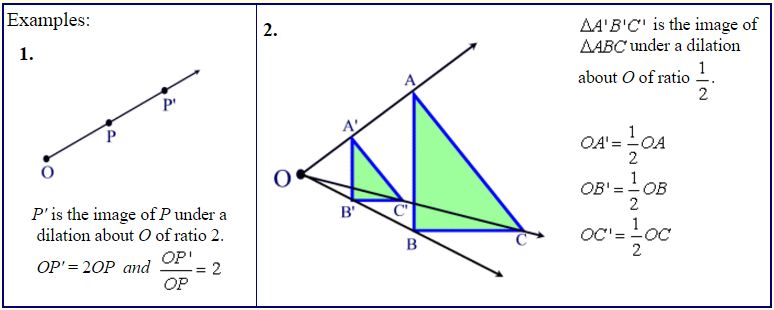Most dilations in coordinate geometry use the origin, (0,0), as the center of the dilation.

Example 1:
Problem: Draw the dilation image of triangle ABC with the center of dilation at the origin and a scale factor of 2.
Observe: Notice how EVERY coordinate of the original triangle has been multiplied by the scale factor (x2).
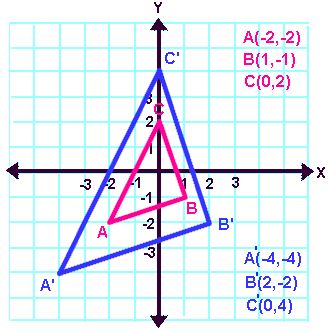Hint: Dilations involve multiplication!

Example 2:
Problem: Draw the dilation image of pentagon ABCDE with the center of dilation at the origin and a scale factor of 1/3.
Observe: Notice how EVERY coordinate of the original pentagon has been multiplied by the scale factor (1/3).
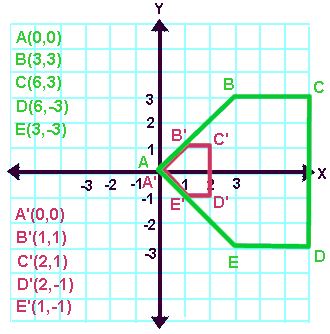Hint: Multiplying by 1/3 is the same as dividing by 3!

For this example, the center of the dilation is NOT the origin. The center of dilation is a vertex of the original figure.

Example 3:
Problem: Draw the dilation image of rectangle EFGH with the center of dilation at point E and a scale factor of 1/2.
Observe: Point E and its image are the same. It is important to observe the distance from the center of the dilation, E, to the other points of the figure. Notice EF = 6 and E’F’ = 3.
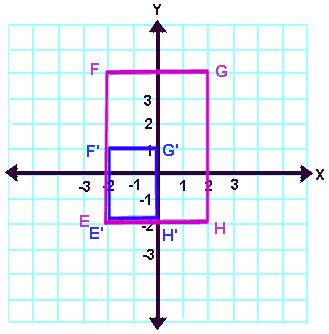Hint: Be sure to measure distances for this problem.