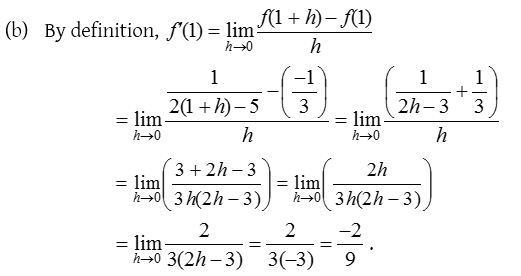Differentiable Function

Differentiable Function

Differentiability of a function at a point

The function, f(x) is differentiable at point P, iff there exists a unique tangent at point P. In other words, f(x) is differentiable at a point P iff the curve does not have P as a corner point. i.e., “the function is not differentiable at those points on which function has jumps (or holes) and sharp edges.”
Let us consider the function f(x) = |x – 1|, which can be graphically shown below.

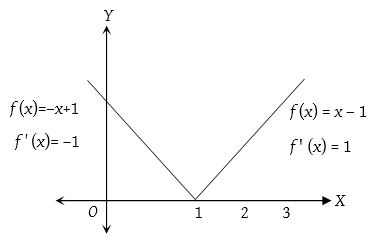
Which show f(x) is not differentiable at x = 1. Since, has sharp edge at x = 1.

Some standard results on differentiability

1. Every polynomial function is differentiable at each x ∈ R.
2. The exponential function a^x, a > 0 is differentiable at each x ∈ R.
3. Every constant function is differentiable at each x ∈ R.
4. The logarithmic function is differentiable at each point in its domain.
5. Trigonometric and inverse trigonometric functions are differentiable in their domains.
6. The sum, difference, product and quotient of two differentiable functions is differentiable.
7. The composition of differentiable function is a differentiable function.

Differentiable Function Problems with Solutions

1.

Solution:

2.

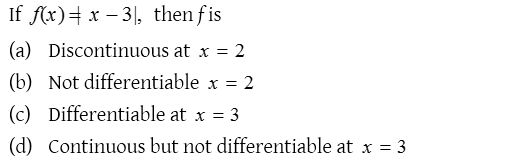
Solution:

3.

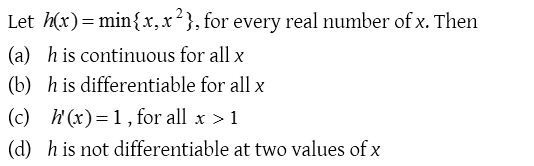
Solution:

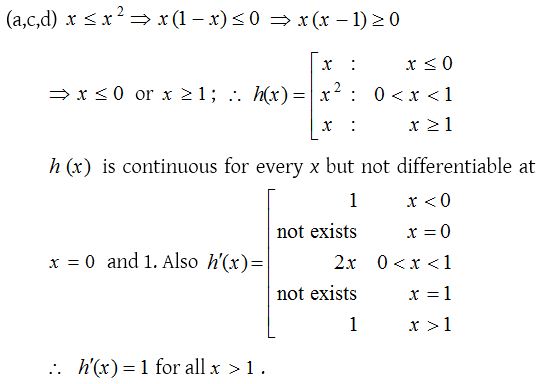
4.

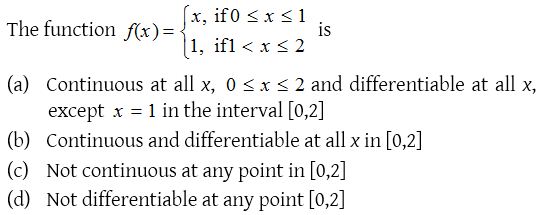
Solution:

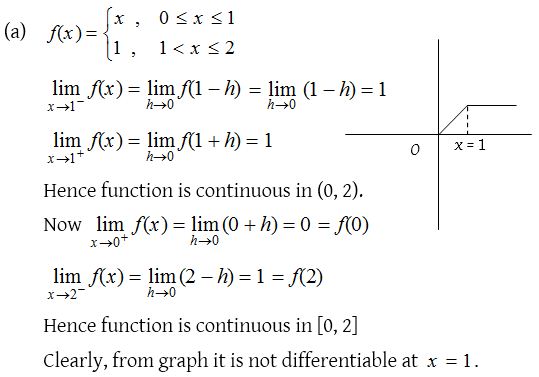
5.

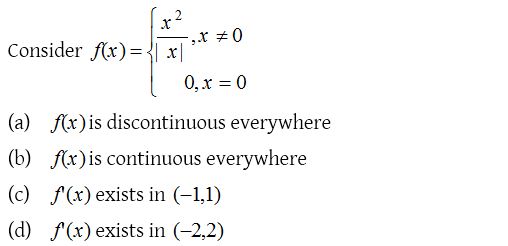
Solution:

6.

Solution:

7.

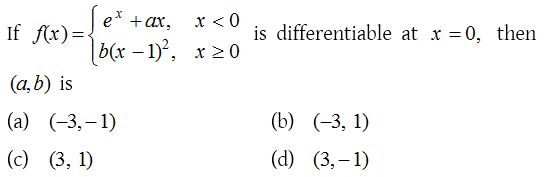
Solution:

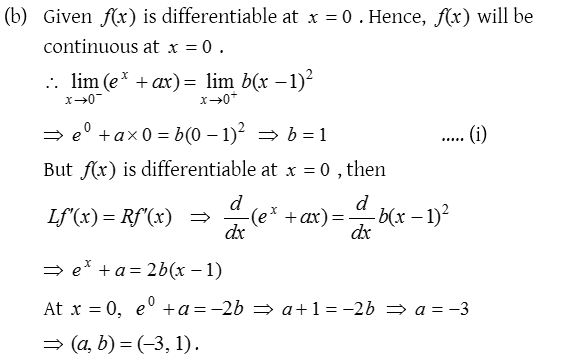
8.

Solution:

9.

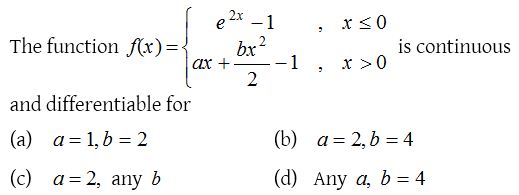
Solution:

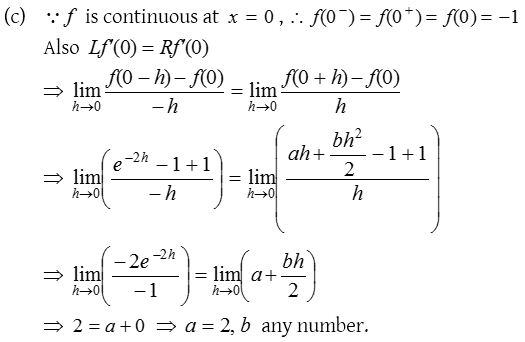
10.

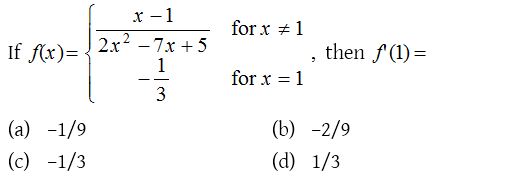
Solution: