Definite Integrals

Let ?(x) be the primitive or anti-derivative of a function f(x) defined on [a, b] i.e., $\frac { d }{ dx } [\phi (x)]=f(x)$ . Then the definite integral of f(x) over [a,b] is denoted by $\int _{ a }^{ b }{ f(x)dx }$ and is defined as [?(b) − ?(a)] i.e., $\int _{ a }^{ b }{ f(x)dx } =\phi (b)-\phi (a)$ . This is also called Newton Leibnitz formula.

The numbers a and b are called the limits of integration, ‘a’ is called the lower limit and ‘b’ the upper limit. The interval [a, b] is called the interval of integration. The interval [a, b] is also known as range of integration. Every definite integral has a unique value.

Evaluation of definite integral by substitution

When the variable in a definite integral is changed, the substitutions in terms of new variable should be effected at three places.
(i) In the integrand (ii)In the differential i.e., dx (iii) In the limits

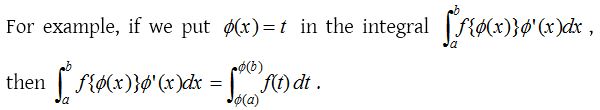
Properties of definite integral

Generally this property is used when the integrand has two or more rules in the integration interval.
This is useful when is not continuous in [a, b] because we can break up the integral into several integrals at the points of discontinuity so that the function is continuous in the sub-intervals.

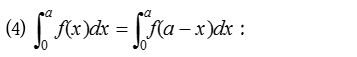
This property can be used only when lower limit is zero. It is generally used for those complicated integrals whose denominators are unchanged when x is replaced by (a – x).
Following integrals can be obtained with the help of above property.

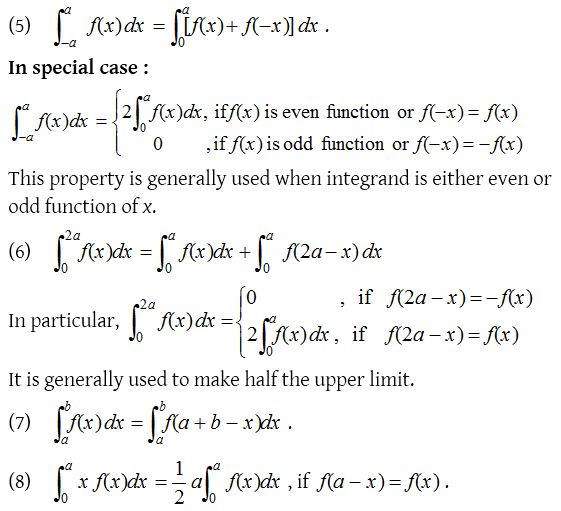
Summation of series by integration

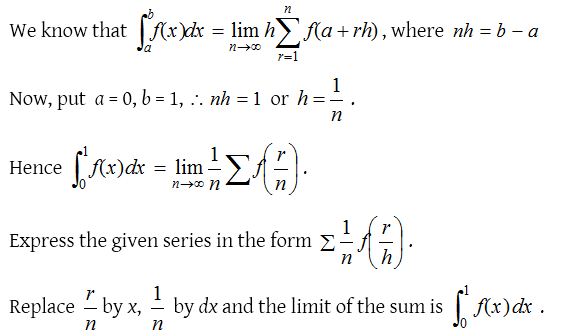
Gamma function

It is important to note that we multiply by (π/2); when both m and n are even.

Reduction formulae for definite integration

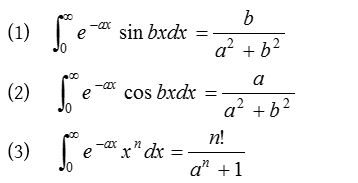
Walli’s formula

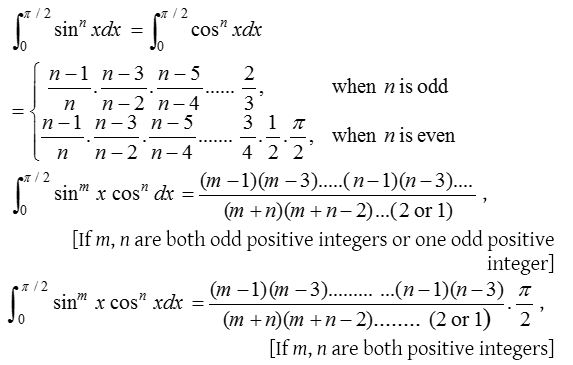
Leibnitz’s rule

(1) If f(x) is continuous and u(x), v(x) are differentiable functions in the interval [a, b], then,

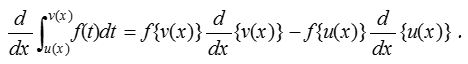
(2) If the function and are defined on [a, b] and differentiable at a point and is continuous, then,

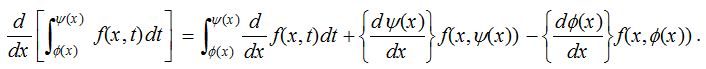
Some important results of definite integral

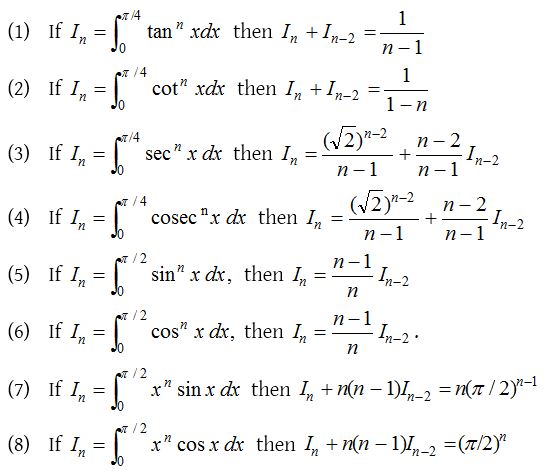
Integration of piecewise continuous functions

Any function f(x) which is discontinuous at finite number of points in an interval [a, b] can be made continuous in sub-intervals by breaking the intervals into these subintervals. If f(x) is discontinuous at points x₁, x₂, x₃, ………. x_n in (a, b), then we can define subintervals (a, x₁), (x₁, x₂) ……… (x_n-1, x_n), (x_n, b) such that f(x) is continuous in each of these subintervals. Such functions are called piecewise continuous functions. For integration of piecewise continuous function, we integrate f(x) in these sub-intervals and finally add all the values.