What is the De' Moivre's Theorem?

What is the De’ Moivre’s Theorem?

(1) If n is any rational number, then (cos θ + i sin θ)ⁿ = cos nθ + i sin nθ.
(2) If z = (cos θ₁ + i sin θ₁) (cos θ₂ + i sin θ₂) (cos θ₃ + i sin θ₃)………… (cos θ_n + i sin θ_n)
then z = cos (θ₁ + θ₂ + θ₃ + ……… + θ_n) + i sin (θ₁ + θ₂ + θ₃ + ……… + θ_n)
where θ₁ + θ₂ + θ₃ + ……… + θ_n ∈ R.
(3) If z = r(cos θ + i sin θ) and n is a positive integer, then

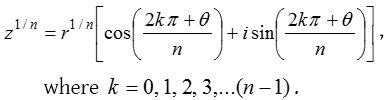
Deductions:

If n ∈ Q, then
(i) (cos θ − i sin θ)ⁿ = cos nθ − i sin nθ
(ii) (cos θ + i sin θ)^-n = cos nθ − i sin nθ
(iii)  (cos θ − i sin θ)^-n = cos nθ + i sin nθ

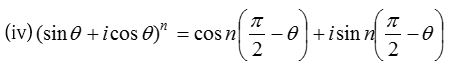
This theorem is not valid when n is not a rational number or the complex number is not in the form of cos θ + i sin θ.

Roots of a complex number

(1) n^th roots of complex number (z^1/n)
Let z = r(cos θ + i sin θ) be a complex number. By using De’moivre’s theorem n^th roots having n distinct values of such a complex number are given by

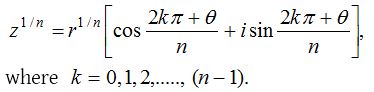
Properties of the roots of z^1/n
(i) All roots of z^1/n are in geometrical progression with common ratio e^2πi/n.
(ii) Sum of all roots of z^1/n is always equal to zero.
(iii) Product of all roots of z^1/n = (−1)^n-1 z.
(iv) Modulus of all roots of z^1/n are equal and each equal to r^1/n or |z|^1/n
(v) Amplitude of all the roots of z^1/n are in A.P. with common difference 2π/n.
(vi) All roots of z^1/n lies on the circumference of a circle whose centre is origin and radius equal to |z|^1/n. Also these roots divides the circle into n equal parts and forms a polygon of n sides.

(2) The n^th roots of unity
The n^th roots of unity are given by the solution set of the equation

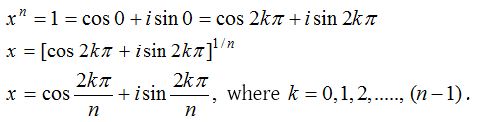
Properties of n^th roots of unity

(i) Let 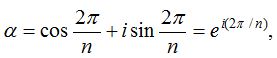 the n^th roots of unity can be expressed in the form of a series i.e., 1, α, α², ….. α^n-1. Clearly the series is G.P. with common ratio α i.e., e^i(2π/n).
(ii) The sum of all n roots of unity is zero i.e., 1, α, α², ….. α^n-1 = 0.
(iii) Product of all n roots of unity is (−1)^n-1.
(iv) Sum of p^th power of n roots of unity

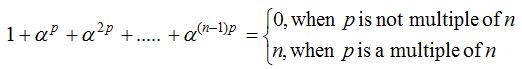
(v) The n, n^th roots of unity if represented on a complex plane locate their positions at the vertices of a regular polygon of n sides inscribed in a unit circle having centre at origin, one vertex on positive real axis.

If one of the complex root is then other root will be or vice-versa.

Properties of cube roots of unity

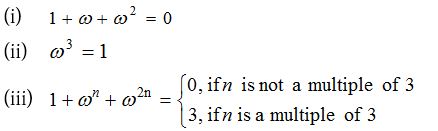
(iv) The cube roots of unity, when represented on complex plane, lie on vertices of an equilateral triangle inscribed in a unit circle having centre at origin, one vertex being on positive real axis.
(v) A complex number a + ib, for which |a : b|= 1 : √3 or √3 : 1, can always be expressed in terms of i, ω, ω².
(vi) Cube root of –1 are −1, −ω, −ω².

(4)  Fourth roots of unity : The four, fourth roots of unity are given by the solution set of the equation x⁴ − 1 = 0.
⇒ (x² – 1)(x² + 1) = 0 ⇒ x = ±1, ±i
Fourth roots of unity are vertices of a square which lies on coordinate axes.