Cylinders
Cylinders are three-dimensional closed surfaces.
In general use, the term cylinder refers to a right circular cylinder with its ends closed to form two circular surfaces, that lie in parallel planes.
Cylinders are not called polyhedra since their faces are not polygons. In many ways, however, a cylinder is similar to a prism. A cylinder has parallel congruent bases, as does a prism, but the cylinder’s bases are circles rather than polygons.
The volume of a cylinder can be calculated in the same manner as the volume of a prism: the volume is the product of the base area times the height of the cylinder, V = Bh.
Since the base in a cylinder is a circle, the formula for the area of a circle can be substituted into the volume formula for B:
V = πr2h
(Volume of a cylinder: r = radius of base, h = height)
A net is a two-dimensional figure that can be cut out and folded up to make a three-dimensional solid.
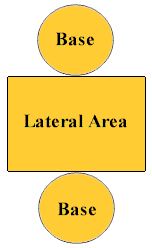Lateral = any face or surface that is not a base.
The surface area (of a closed cylinder) is a combination of the lateral area and the area of each of the bases. When disassembled, the surface of a cylinder becomes two circular bases and a rectangular surface (lateral surface), as seen in the net at the left.
Note that the length of the rectangular surface is the same as the circumference of the base. Remember that the area of a rectangle is length times width.
The lateral area (rectangle) = height × circumference of the base.
The base area = area of a circle (remember there are two bases)
Total Surface Area of a Closed Cylinder SA = 2πrh + 2πr2
which can also be factored and written as SA = 2πr(r+h)
When working with surface areas of cylinders, read the questions carefully.
