Criteria For Congruent Triangles
https://www.youtube.com/watch?v=QkU4FZN8MY0
Congruent triangles are triangles that have the same size and shape. This means that the corresponding sides are equal and the corresponding angles are equal.
Congruent Triangles do not have to be in the same orientation or position. They only have to be identical in size and shape.
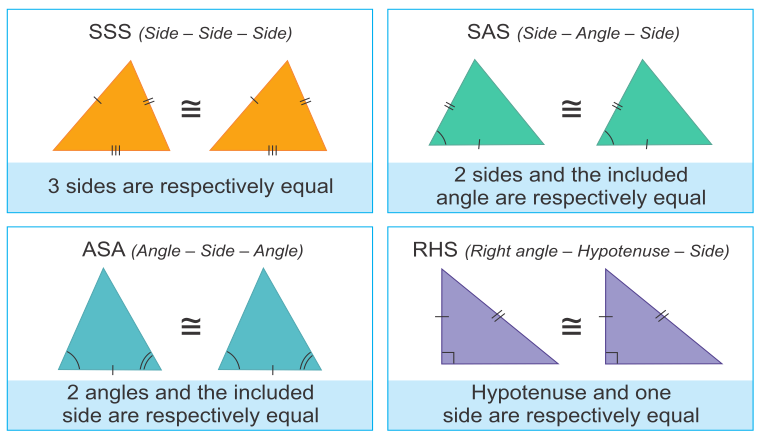
- SSS (Side Side Side) Congruence Criteria (Condition):
Two triangles are congruent, if three sides of one triangle are equal to the corresponding three sides of the other triangle.

∴ By SSS criteria ∆ABC ∆EDF
∴ ∠A = ∠E, ∠B = ∠D, ∠C = ∠F (c.p.c.t.) - ASA (Angle Side Angle) Congruence Criteria (Condition):
Two triangles are congruent, if two angles and the included side of one is equal to the corresponding angles and side of the other.
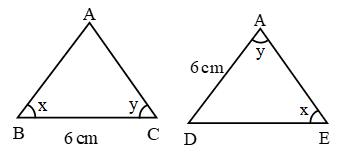
∴ By ASA criteria ∆ABC ≅ ∆DEF
∴ ∠A = ∠D, AB = DE, AC = DF (c.p.c.t.) - AAS (Angle Angle Side) Congruence Criteria (Condition):
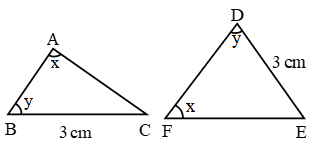
∴ By AAS, ∆ABC ≅ ∆FDE
∴ ∠C = ∠E, AB = FD, AC = FE (c.p.c.t.) - SAS (Side Angle Side) Congruence Criteria (Condition):
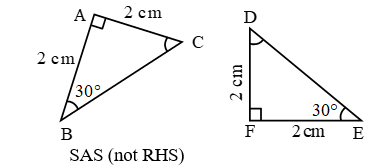
When two sides and the included angle of one triangle is equal to the corresponding sides and the included angle of another triangle, the two triangles are congruent. This, condition of congruence is known as side-angle-side congruence. In short we write SAS condition.
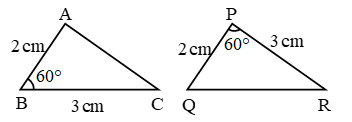
By SAS, ∆ABC ≅ ∆QPR
∴ ∠A = ∠Q, ∠C = ∠R, AC = QR (c.p.c.t.) - RHS (Right Hypotenuse Side) Congruence Criteria (Condition):
Two right triangles are congruent, if the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.
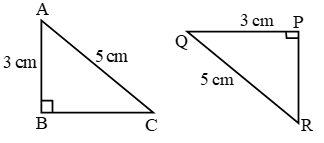
∴ By RHS, ∆ABC ≅ ∆QPR
∴ ∠A = ∠Q, ∠C = ∠R, BC = PR (c.p.c.t.)
Example 1:
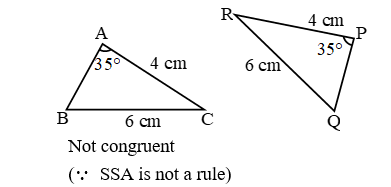
Example 2:
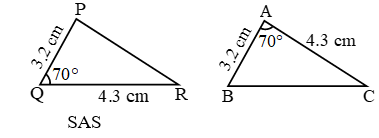
Example 3:
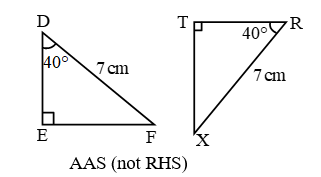
Example 4:
Read More:
- How Do You Prove Triangles Are Congruent
- RS Aggarwal Class 7 Maths Solutions Congruence
- RS Aggarwal Class 9 Solutions Congruence of Triangles and Inequalities in a Triangle
Theorem 1: If two angles and the included side of one triangle are equal to two angles and the included side of other triangle, then both triangles are congruent.
Proof:
Given: ∆ABC and ∆DEF in which
∠ABC = ∠DEF, ∠ACB = ∠DFE and BC = EF.
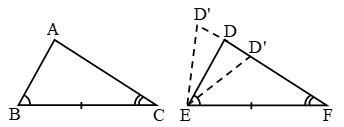
To Prove: ∆ABC ≅ ∆DEF.
Proof:
Case I:
Let AC = DF.
In this case, AC = DF, BC = EF and ∠C = ∠F.
∴ ∆ABC ≅ ∆DEF (SAS-criteria)
Case II:
If possible, let AC ≠ DF.
Then, construct D’ F = AC. Join D’ E.
Now, in ∆ABC and ∆D’EF, we have AC = D’F, BC = EF and ∠C = ∠F.
∴ ∆ABC ∆D’EF (SAS-criteria)
∴ ∠ABC = ∠D’EF (c.p.c.t)
But, ∠ABC = ∠DEF (given)
∴ ∠D’EF = ∠DEF.
This is possible only when D and D’ coincide.
∴ ∆ABC ≅ ∆DEF.
Theorem 2: Two right-angled triangles are congruent if one side and the hypotenuse of the one are respectively equal to the corresponding side and the hypotenuse of the other. (i.e. RHS)
Given: Two right-angled triangles ∆ABC & ∆DEF in which ∠B = ∠E = 90°, BC = EF and AC = DF.
To Prove: ∆ABC ≅ ∆DEF.
Construction: Produce DE to G such that
GE = AB. Join GF.
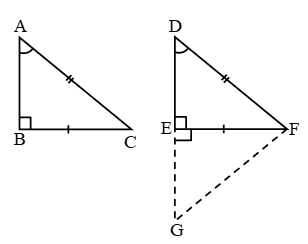
Proof: In ∆ABC and ∆GEF, we have:
AB = GE (construction),
BC = EF (given),
∠B = ∠FEG = 90°
⇒ ∆ABC ∆GEF (SAS-criteria)
⇒ ∠A = ∠G and AC = GF (c.p.c.t.)
Now, AC = GF and AC = DF ⇒GF = DF
⇒ ∠G = ∠D ⇒ ∠A = ∠D [∵ ∠G = ∠A]
Now, ∠A = ∠D, ∠B = ∠E ⇒ 3rd ∠C = 3rd ∠F.
Thus, in ∆ABC and ∆DEF, we have:
BC = EF, AC = DF and ∠C = ∠F.
∴ ∆ABC ≅ ∆DEF (SAS-criteria).
Criteria For Congruent Triangles Example Problems With Solutions
Example 1: Prove that diagonal of a parallelogram divides it into two congruent triangles.
Solution: Let ABCD is a parallelogram and AC is a diagonal.
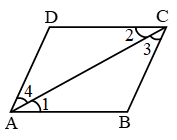
(By SSS): In ∆ABC and ∆ADC
AB = CD (opp. sides of ||gm)
BC = AD (opp. sides of ||gm)
AC = AC (common)
∴ By SSS, ∆ABC ≅ ∆CDA proved
{other results : ∠1 = ∠2, ∠3 = ∠4, ∠B = ∠D (c.p.c.t.)}
(By ASA): In ∆ABC and ∆ADC
∠1 = ∠2 (alternate)
AC = AC (common)
∠3 = ∠4 (alternate)
∴ By ASA, ∆ABC ≅ ∆CDA
{other results: ∠B = ∠D, AB = CD, BC = AD (c.p.c.t.)}
(By AAS): In ∆ABC and ∆ADC
∠1 = ∠2 (alternate)
∠3 = ∠4 (alternate)
BC = AD (opp. sides)
∴ ∆ABC ≅ ∆CDA
{other results : AB = CD, ∠B = ∠D, AC = AC (c.p.c.t.)}
(By SAS): In ∆ABC and ∆ADC
AB = CD (opp. sides of ||gm)
∠1 = ∠2 (alternate)
AC = AC (common)
∴ ∆ABC ≅ ∆CDA
{other results: ∠3 = ∠4, BC = AD, ∠B = ∠D (c.p.c.t.)
We can not use ‘RHS’ for this proof.
Note: ASS or SSA criteria for congruency is not valid.
Example 2: In Fig. it is given that AB = CF, EF = BD and ∠AFE = ∠DBC. Prove that ∆AFE ∆CBD.
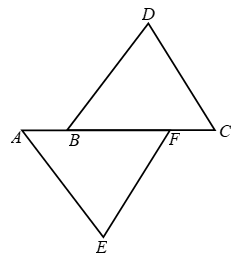
Solution: We have, AB = CF
⇒ AB + BF = CF + BF
⇒ AF = CB …. (i)
In ∆s AFE and CBD, we have
AF = CB [From (i)]
∠AFE = ∠DBC [Given]
and EF = BD [Given]
So, by SAS criterion of congruence, we have
∆AFE ≅ ∆CBD
Example 3: In Fig. X and Y are two points on equal sides AB and AC of a ∆ABC such that AX = AY. Prove that XC = YB.
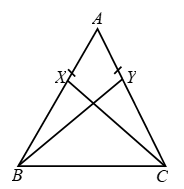
Solution: In ∆s AXC and AYB, we have
AX = AY [Given]
∠A = ∠A [Common angle]
AC = AB [Given]
So, by SAS criterion of congruene
∆AXC ≅ ∆AYB
⇒ XC = YB (c.p.c.t.)
Example 4: In Fig. PQRS is a quadrilateral and T and U are respectively points on PS and RS such PQ = RQ, ∠PQT = ∠RQU and ∠TQS = ∠UQS. Prove that QT = QU.
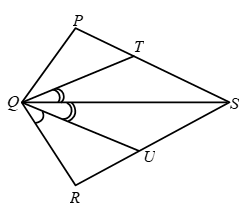
Solution: We have,
∠PQT = ∠RQU
and, ∠TQS = ∠UQS
∴ ∠PQT + ∠TQS = ∠RQU + ∠UQS
⇒ ∠PQS = ∠RQS …. (i)
Thus, in triangles PQS and RQS, we have
PQ = RQ [Given]
∠PQS = ∠RQS [From (i)]
and, QS = QS [Common side]
Therefore, by SAS congruence criterion, we have
∆PQS ≅ ∆RQS
⇒ ∠QPS = ∠QRS (c.p.c.t.)
⇒ ∠QPT = ∠QRU …. (ii)
Now, consider triangles QPT and QRS. In these two triangles, we have
QP = QR [Given]
∠PQT = ∠RQU [Given]
∠QPT = ∠QRU [From (ii)]
Therefore, by ASA congruence criterion, we get
∆QPT ≅ ∆QRU
⇒ QT = QU.
Example 5: In Fig. PS = QR and ∠SPQ = ∠RQP.
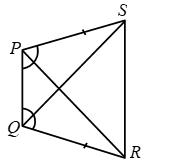
Prove that PR = QS and ∠QPR = ∠PQS.
Solution: In ∆SPQ and ∆RQP, we have
PS = QR [Given]
∠SPQ = ∠RQP [Given]
PQ = PQ [Common]
Therefore, by SAS criterion of congruence, we have
∆SPQ ∆RQP ⇒ SQ = RP and
∠QPR = ∠PQS
Example 6: ∆ABC is an isosceles triangle with AB = AC. Side BA is produced to D such that
AB = AD. Prove that ∠BCD is a right angle.
Solution: Given : A ∆ABC such that AB = AC. Side BA is produced to D such that AB = AD.
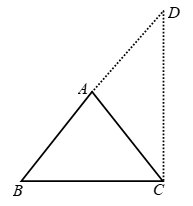
Construction : Join CD.
To prove : ∠BCD = 90º
Proof : In ∆ABC, we have AB = AC
⇒ ∠ACB = ∠ABC …(i) [∵ Angles opp. to equal sides are equal]
Now, AB = AD [Given]
∴ AD = AC [∴ AB = AC]
Thus, in ∆ADC, we have
AD = AC
⇒ ∠ACD = ∠ADC …(ii)
[∵ Angles opp. to equal sides are equal]
Adding (i) and (ii), we get
∠ACB + ∠ACD = ∠ABC + ∠ADC
⇒ ∠BCD = ∠ABC + ∠BDC
[∵ ∠ADC = ∠BDC, ∠ABC = ∠DBC]
⇒ ∠BCD + ∠BCD = ∠DBC + ∠BCD + ∠BDC
[adding ∠BCD on both sides ]
⇒ 2 ∠BCD = 180º
[∵ Sum of the angles of a ∆ is 180º]
Hence, ∠BCD is a right angle.
Example 7: In Fig. AC = BC, ∠DCA = ∠ECB and ∠DBC = ∠EAC.
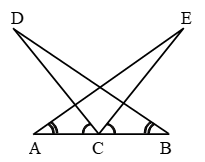
Prove that triangles DBC and EAC are congruent, and hence DC = EC.
Solution: We have,
∠DCA = ∠ECB
⇒ ∠DCA + ∠ECD = ∠ECB + ∠ECD
⇒ ∠ECA = ∠DCB …. (i)
Now, in ∆s DBC and EAC, we have
∠DCB = ∠ECA [From (i)]
BC = AC [Given]
and ∠DBC = ∠EAC [Given]
So, by ASA criterion of congruence
∆DBC ≅ ∠EAS
⇒ DC = EC (c.p.c.t.)
Example 8: If the altitudes from two vertices of a triangle to the opposite sides are equal, prove that the triangle is isosceles.
Solution: Given: A ∆ABC in which altitudes BE and CF from B and C respectively on AC and AB are equal.
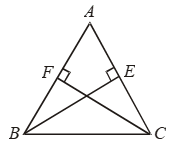
To prove: ∆ABC is isoceles i.e. AB = AC
Proof: In ∆s ABC and ACF, we have
∠AEB = ∠AFC [Each equal to 90º]
∠BAE = ∠CAF [Common angle]
and, BE = CF [Given]
So, by AAS criterion of congurence, we have
∆ABE ≅ ∆ACF
⇒ AB = AC [∵ Corresopnding parts of congruent triangles are equal]
Hence, ∆ABC is isosceles.
Example 9: In ∆ABC, AB = AC and the bisectors of angles B and C intersect at point O. Prove that BO = CO and the ray AO is the bisector of angle BAC.
Solution: In ∆ABC, we have
AB = AC
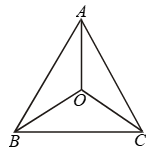
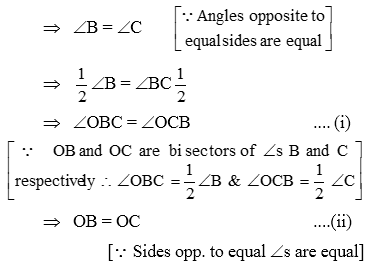
Now, in ∆ABO and ∆ACO, we have
AB = AC [Given]
∠OBC = ∠OCB [From (i)]
OB = OC [From (ii)]
So, by SAS criterion of congruence
∆ABO ≅ ∆ACO
⇒ ∠BAO = ∠CAO
[∵ Corresponding parts of congruent triangles are equal]
⇒ AO is the bisector of ∠BAC.
Example 10: In Fig. BM and DN are both perpendiculars to the segments AC and BM = DN.
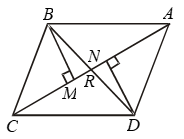
Prove that AC bisects BD.
Solution: In ∆s BMR and DNR, we have
∠BMR = ∠DNR
[Each equal to 90º ∵ BM ⊥ AC and DN ⊥ AC]
∠BRM = ∠DRN [Vert. opp. angles]
and, BM = DN [Given]
So, by AAS criterion of congruence
∆BMR ≅ ∆DNR
⇒ BR = DR
[∵ Corresponding parts of congruent triangles are equal]
⇒ R is the mid-point of BD.
Hence, AC bisects BD.
Example 11: In Fig. BD and CE are two altitudes of a ∆ABC such that BD = CE.
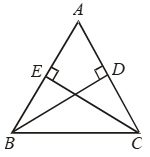
Prove that ∆ABC is isolceles.
Solution: In ∆ABD and ∆ACE, we have
∠ADB = ∠AEC = 90º [Given]
∠BAD = ∠CAE [Common]
and, BD = CE [Given]
So, by AAS congruence criterion, we have
∆ABD ≅ ∆ACE
⇒ AB = AC [∵ Corresponding parts of congruent triangles are equal]
Hence, ∆ABC is isosceles.
Example 12: If two isosceles triangles have a common base, the line joining their vertices bisects them at right angles.
Solution: Given: Two isosceles triangles ABC and DBC having the common base BC such that AB = AC and DB = DC.
To prove: AD (or AD produced) bisects BC at right angle.
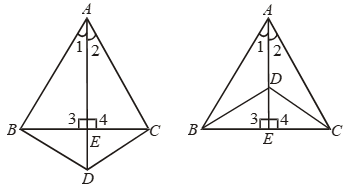
Proof : In ∆s ABD and ACD, we have
AB = AC [Given]
BD = CD [Given]
AD = AD [Common side]
So, by SSS criterion of congruence
∆ABD ≅ ∆ACD
⇒ ∠1 = ∠2 …. (i)
[∵ Corresponding parts of congruent triangles are equal]
Now, in ∆s ABE and ACE, we have
AB = AC [Given]
∠1 = ∠2 [From (i)]
and, AE = AE [Commoni side]
So, by SAS criterion of congruence,
∆ABE ≅ ∆ACE
⇒ BE = CE
[∵ Corresponding parts of congruent triangles are equal]
and, ∠3 = ∠4
But, ∠3 + ∠4 = 180º
[∵ Sum of the angles of a linear pair is 180º]
⇒ 2 ∠3 = 180º [∵ ∠3 = ∠4]
⇒ ∠3 = 90º
∴ ∠3 = ∠4 = 90º
Hence, AD bisects BC at right angles.
Example 13: AD, BE and CF, the altitudes of ∆ABC are equal. Prove that ∆ABC is an equilateral triangle
Solution: In right triangles BCE and BFC, we have
Hyp. BC = Hyp. BC
BE = CF [Given]
So, by RHS criterion of congruence,
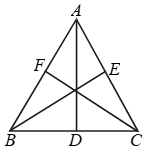
∆BCE ∆BFC.
⇒ ∠B = ∠C [∵ Corresponding parts of congruent triangles are equal]
⇒ AC = AB …. (i)
[∵ Sides opposite to equal angles are equal]
Similarly, ∆ABD ≅ ∆ABE
⇒ ∠B =∠A
[Corresponding parts of congruent triangles are equal]
⇒ AC = BC …. (ii)
[Sides opposite to equal angles are equal]
From (i) and (ii), we get
AB = BC = AC
Hence, ∆ABC is an equilateral triangle.
Example 14: In Fig. AD = BC and BD = CA.
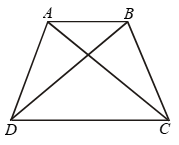
Prove that ∠ADB = ∠BCA and
∠DAB = ∠CBA.
Solution: In triangles ABD and ABC, we have
AD = BC [Given]
BD = CA [Given]
and AB = AB [Common]
So, by SSS congruence criterion, we have
∆ABD ∠CBA ⇒ ∠DAB = ∠ABC
[∵ Corresponding parts of congruent triangles are equal]
⇒ ∠DAB = ∠CBA
Example 15: Line-segment AB is parallel to another line-segment CD. O is the mid-point of AD (see figure). Show that (i) ∆AOB ≅ ∆DOC (ii) O is also the mid point of BC.
Solution: (i) Consider ∆AOB and ∆DOC
∠ABO = ∠DCO
(Alternate angles as AB || CD and BC is the transversal)
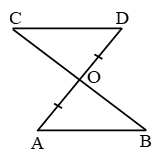
∠AOB = ∠DOC (Vertically opposite angles)
OA = OD (Given)
Therefore, ∆AOB ≅ ∆DOC (AAS rule)
(ii) OB = OC (c.p.c.t.)
So, O is the mid-point of BC.
Example 16: In quadrilateral ABCD, AC = AD and AB bisects ∠A. Show that ∆ABC ∆ABD. What can you say about BC and BD ?
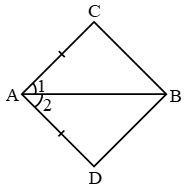
Solution: In ∆ABC & ∆ABD
AB = AB (common)
∠1 = ∠2 {∵ AB is bisector of ∠A}
AC = AD (Given)
∴ By SAS, ∆ABC ≅ ∆ABD Proved
also BC = BD (c.p.c.t.)
Example 17: AD and BC are equal perpendiculars to a line segment AB. Show that CD bisects AB.
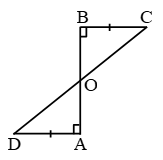
Solution: To show CD bisect AB i.e. AO = OB
∴ in ∆OAD and ∆OBC
∠O = ∠O (vertically opposite angles)
∠A = ∠B = 90° (Given)
AD = BC (Given)
∴ By AAS, ∆OAD ≅ ∆OBC
∴ OA = OB (c.p.c.t.)
∴ CD, bisects AB. Proved
Example 18: Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that
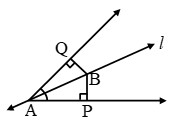
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.
Solution: (i) In ∆APB and ∆AQB
∠P = ∠Q = 90° (Given)
∠PAB = ∠QAB (Given that ‘l’ bisect ∠A)
AB = AB (Common)
∴ By AAS, ∆APB ≅ ∆AQB. Proved
(ii) BP = BQ (c.p.c.t.) Proved.
Example 19: In given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
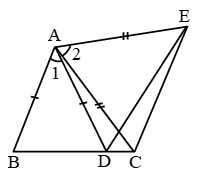
Solution: In ∆ABC and ∆ADE
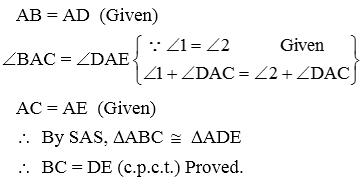
Example 20: In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that:
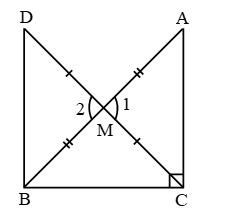
(i) ∆AMC ≅ ∆BMD
(ii) ∠DBC is a right angle
(iii) ∆DBC ≅ ∆ACB
(iv) CM = AB
Solution: (i) In ∆AMC and ∆BMD
AM = MB (M is mid point of AB)
∠1 = ∠2 (vertically opposite angles)
CM = MD (given)
∴ By SAS, ∆AMC ≅ ∆MBD Proved.
(ii) ∠ACM = ∠MDB (c.p.c.t. of (i))
These are alternate angles
∴ DB || AC
So ∠DBC + ∠ACB = 180°
(Cointerior angles)
⇒ ∠DBC + 90° = 180°
⇒ ∠DBC = 90° Proved.
(iii) In ∆DBC & ∆ACB
BC = BC ( common)
∠DBC = ∠ACB = 90°
DB = AC (c.p.c.t. of part (i))
∴ By SAS, ∆DBC ≅ ∆ACB. Proved
(iv) DC = AB (c.p.c.t. of part (iii))
But CM = DC (given)
∴ CM = AB Proved.
