Construct a Line Segment and an Angle
A reference line is a line upon which you produce copies of existing figures.
Construct a line segment
Given: (Line segment) \(\overline { AB }\)
Task: To construct a line segment congruent to (line segment) \(\overline { AB }\).
Directions:
- If a reference line does not already exist, draw a reference line with your straightedge upon which you will make your construction. Place a starting point on the reference line.
- Place the point of the compass on point A.
- Stretch the compass so that the pencil is exactly on B.
- Without changing the span of the compass, place the compass point on the starting point on the reference line and swing the pencil so that it crosses the reference line. Label your copy.
Your copy and (line segment) are congruent. Congruent means equal in length.
Explanation of construction: The two line segments are the same length, therefore they are congruent.
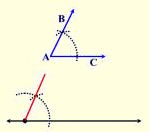
Construct an angle
Given: ∢BAC
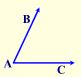Task: To construct an angle congruent to ∢BAC.
Directions:
- If a reference line does not already exist, draw a reference line with your straightedge upon which you will make your construction. Place a starting point on the reference line.
- Place the point of the compass on the vertex of ∢BAC (point A).
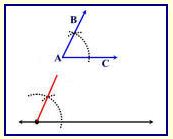
- Stretch the compass to any length so long as it stays ON the angle.
- Swing an arc with the pencil that crosses both sides of ∢BAC.
- Without changing the span of the compass, place the compass point on the starting point of the reference line and swing an arc that will intersect the reference line and go above the reference line.
- Go back to ∢BAC and measure the width (span) of the arc from where it crosses one side of the angle to where it crosses the other side of the angle.
- With this width, place the compass point on the reference line where your new arc crosses the reference line and mark off this width on your new arc.
- Connect this new intersection point to the starting point on the reference line.
Your new angle is congruent to ∢BAC.
Explanation of construction: When this construction is finished, draw a line segment connecting where the arcs cross the sides of the angles. You now have two triangles that have 3 sets of congruent (equal) sides. SSS is sufficient to prove triangles congruent. Since the triangles are congruent, any leftover corresponding parts are also congruent – thus, the angle on the reference line and ∢BAC are congruent.
