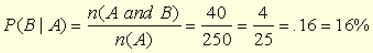Conditional Probability
The conditional probability of an event B, in relation to event A, is the probability that event B will occur given the knowledge that an event A has already occurred.

In plain English …
You toss two pennies. The first penny shows HEADS and the other penny rolls under the table and you cannot see it. Now, what is the probability that they are both HEADS? Since you already know that one is HEADS, the probability of getting HEADS on the second penny is 1 out of 2.
The probability changes if you have partial information.
This “affected” probability is called conditional probability.
Notation for conditional probability: \(P(\frac { B }{ A } )\)
read … the probability of B given A.
To establish our formulas for conditional probability, we will need to revisit our previous discussion of independent and dependent events.
If events A and B are independent (where event A has no effect on the probability of event B), then the conditional probability of event B given event A is simply the probability of event B.
Example: Two colored dice (one blue, one yellow) are rolled.
a. What is the probability of rolling “box cars” (two sixes) is \(\frac { 1 }{ 6 } \times \frac { 1 }{ 6 } =\frac { 1 }{ 36 }\)?
b. What is the probability of rolling “box cars” knowing the first toss is a six?
Answer:
a. The probability of getting “box cars” (two sixes) is \(\frac { 1 }{ 6 } \).
b. If, however, we roll the dice and and see that the blue die shows a six (and the yellow die is out of sight), the probability of the yellow die being six is .
The probability of rolling “box cars”, knowing that the first roll is a six, is \(\frac { 1 }{ 6 } \).
The probability changes when you have partial information about the situation.
If events A and B are dependent (where event A has effect on the probability of event B), then we saw that the probability that both events occur is defined by:
\(P(A\quad and\quad B)=P(A)\times P(\frac { B }{ A } )\)
Dividing both sides of this equation by P(A) gives us our formula for conditional probability of event B given event A, where event A affects the probability of event B:
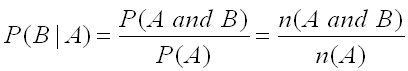
Assuming P(A), n(A) are not zero.
Example 1: A bag contains 12 red M&Ms, 12 blue M&Ms, and 12 green M&Ms. What is the probability of drawing two M&Ms of the same color in a row?
Answer:
Intuitive: There are a total of 36 M&Ms in the bag. You draw a blue M&M and eat it. There are now 11 blue M&Ms remaining in the bag. There are 35 total M&Ms now remaining. You will now need to draw another blue M&M. The conditional probability will be:
P(Draw blue M&M | First M&M was blue) = \(\frac { 11 }{ 35 }\).
Using the formula:
P(A and B) = \(\frac { 12 }{ 36 } \times \frac { 11 }{ 35 } \)
P(A) = \(\frac { 12 }{ 36 }\)
P(Draw same as first color M&M | First M&M color)
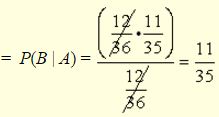
Example 2: In a school of 1200 students, 250 are seniors, 150 students take math, and 40 students are seniors and are also taking math. What is the probability that a randomly chosen student who is a senior, is taking math?
Answer: These questions can be confusing. It sounds, at first read, that they are asking for the probability of choosing a student who is a senior and who is taking math. Not quite right!
It helps to re-word the question into:
Find the probability that the student is taking math, given that the student is a senior.
B = the student is taking math
n(A) = the student is a senior = 250.
n(A and B) = the student is a senior and is taking math = 40.