Concurrence
Lines that contain the same point are called concurrent. Concurrence is the concept of three or more lines intersecting in a single (common) point, having a single point of intersection.
Medians
A median of a triangle is a segment joining any vertex to the midpoint of the opposite side. The medians of a triangle are concurrent. Notice that the point of concurrence is in the interior of the triangles.
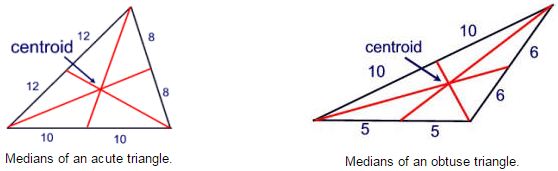 Archimedes showed that the point where the medians are concurrent is the center of gravity of a triangular shape of uniform thickness and density. This point where the medians are concurrent is called the centroid of a triangle. If you cut a triangle out of cardboard and balance it on a pointed object, such as a pencil, the pencil will mark the location of the triangle’s centroid.
Archimedes showed that the point where the medians are concurrent is the center of gravity of a triangular shape of uniform thickness and density. This point where the medians are concurrent is called the centroid of a triangle. If you cut a triangle out of cardboard and balance it on a pointed object, such as a pencil, the pencil will mark the location of the triangle’s centroid.
The centroid divides the medians into a 2:1 ratio. The section of the median nearest the vertex is twice as long as the section near the midpoint of the triangle’s side.
Altitudes
An altitude of a triangle is a segment from any vertex perpendicular to the line containing the opposite side. The lines containing the altitudes of a triangle are concurrent. Notice that the point of concurrence is not necessarily inside the triangle.
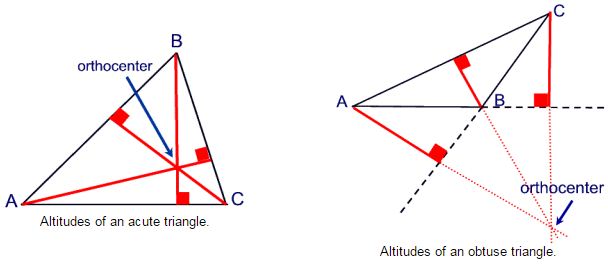 The point where the lines containing the altitudes are concurrent is called the orthocenter of a triangle. (The prefix “ortho” means “right”.)
The point where the lines containing the altitudes are concurrent is called the orthocenter of a triangle. (The prefix “ortho” means “right”.)
Angle Bisectors
The angle bisectors of a triangle are concurrent. Notice that the point of concurrence is in the interior of the triangles.
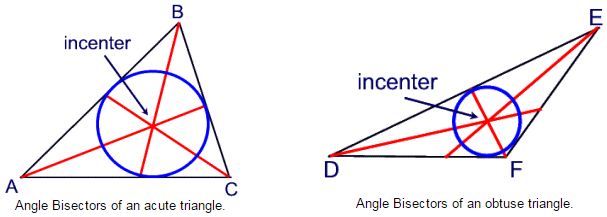 The point of concurrence is the center of an inscribed circle within the triangle. The point of concurrence is called the incenter.
The point of concurrence is the center of an inscribed circle within the triangle. The point of concurrence is called the incenter.
Perpendicular Bisectors
The perpendicular bisectors of the sides of a triangle are concurrent. Notice that the point of concurrence is not necessarily in the interior of the triangles.
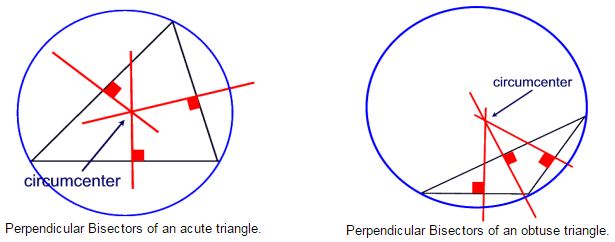 The point of concurrence is the center of a circumscribed circle about the triangle. The point of concurrence is called the circumcenter.
The point of concurrence is the center of a circumscribed circle about the triangle. The point of concurrence is called the circumcenter.
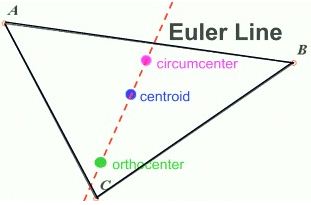
Euler Line
In any triangle, the circumcenter, centroid, and orthocenter are collinear (lie on the same straight line). The collinear line upon which these three points lie is called the Euler line. The centroid is always located between the circumcenter and the orthocenter. The centroid is twice as close to the circumcenter as to the orthocenter.
 The word “Euler” is pronounced as if it were spelled “Oiler” and refers to the mathematician Leonhard Euler (1707-1783).
The word “Euler” is pronounced as if it were spelled “Oiler” and refers to the mathematician Leonhard Euler (1707-1783).
