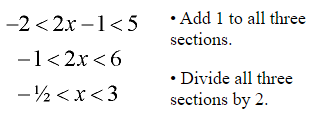Compound Linear Inequalities
Remember the primary rule for working with linear inequalities:
Multiplying or dividing by a negative number changes the direction of the inequality.
A compound inequality is two simple inequalities joined by the word “and” or “or“.
(It is also possible that a compound inequality may contain an inequality and an equation.)
Examples: x < 5 and x > -2 a + 2 > 4 or a + 3 = 6
You will now be seeing more references to interval notation when working with linear inequalities. Check the table below if you need a quick review of this notation.


Solving Compound Linear Inequalities:
Example 1: Solve and graph the solution set of: 3x + 2 < 5 and x + 2 > -4
Solve each inequality separately.
Combine the solutions.
Since this problem is “and”, graph where the solutions intersect with one another.
Note: The solution x < 1 and x > -6 can also be written as -6 < x < 1.
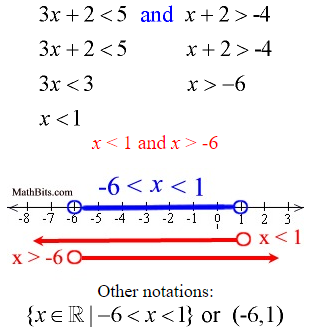
The graph will be the overlapping of the two separate graphs. Graph using an open circle for both -6 and 1 (x can not equal -6 nor 1) since our symbols are simply less than or greater than.
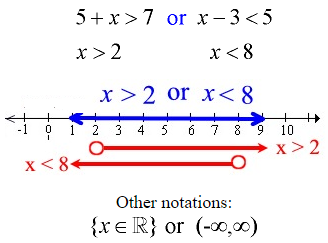
Example 2: Solve and graph the solution set of: 5 + x > 7 or x – 3 < 5
Solve each inequality separately.
Combine the solutions.
Since this problem is “or”, graph where both solutions are true.
Graphing where both solutions are true covers the entire number line. Any number on the number line will make “one” or “both” of the inequaltites true.
Example 3: Solve and graph the solution set of: x < 4 and x ≠ 1
Since this problem is “and”, graph where the two inequalities intersect — where BOTH are true.
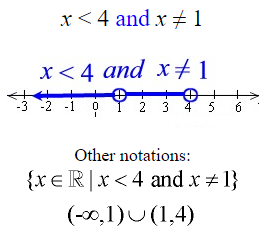
Example 4: Solve and graph the solution set of: 2x – 1 < 5 and 2x – 1 > -2
Solve each inequality separately.
Combine the solutions.
Since this problem is “and”, graph where the solutions intersect with one another.
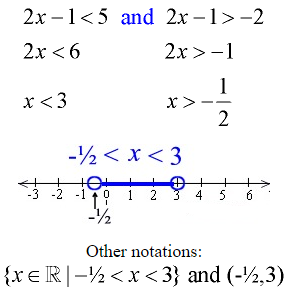
Note: This problem can also be written as -2 < 2x – 1 < 5. When solving for x in this form, be sure to perform any changes to all three components of the inequality.