Composition of Functions (f o g)(x)
The term “composition of functions” (or “composite function”) refers to the combining of functions in a manner where the output from one function becomes the input for the next function.
 In math terms, the range (the y-value answers) of one function becomes the domain (the x-values) of the next function.
In math terms, the range (the y-value answers) of one function becomes the domain (the x-values) of the next function.
The notation used for composition is:
(f o g)(x) = f(g(x)) and is read “f composed with g of x” or “f of g of x”.
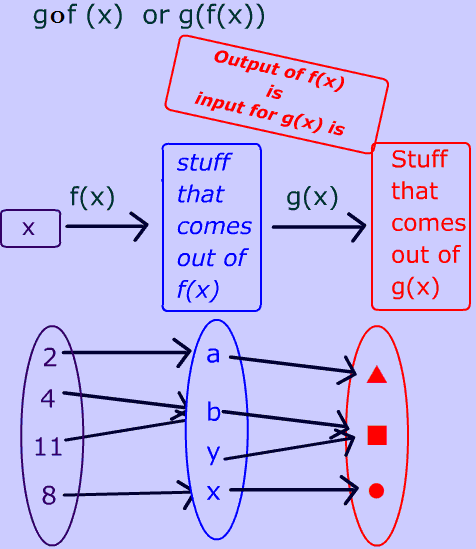
 Notice how the letters stay in the same order in each expression for the composition.
Notice how the letters stay in the same order in each expression for the composition.
f (g(x)) clearly tells you to start with function g (innermost parentheses are done first).
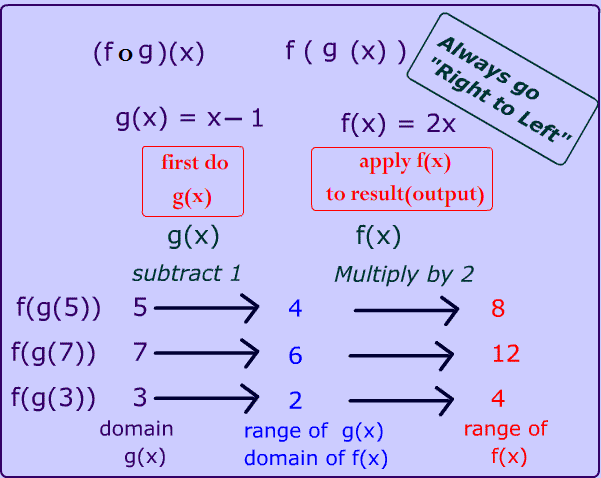
Composition of functions can be thought of as a series of taxicab rides for your values.
The example below shows functions f and g working together to create the composition .
Note: The starting domain for function g is being limited to the four values 1, 2, 3 and 4 for this example.

In the example above, you can see what is happening to the individual elements throughout the composition. Now, suppose that we wish to write our composition as an algebraic expression.
Examples :


