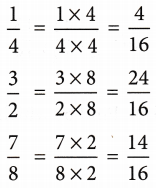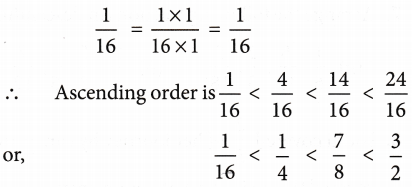What is Comparing and Ordering of Fractions
Comparison of fractions are divided into three categories.
1. Fraction with the same numerator
Let us consider the following fractions with the same numerator: \(\frac{1}{3}\), \(\frac{1}{2}\), \(\frac{1}{6}\)
The pictorial representation of these fractions are given below:
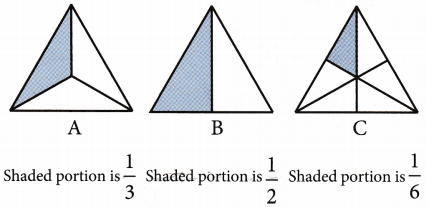
By looking at the shaded portion in these pictures, we can conclude that
shaded area of B > shaded area of A > shaded area of C
or \(\frac{1}{2}\) > \(\frac{1}{3}\) > \(\frac{1}{6}\)
Thus, we conclude that if two or more fractions have the same numerator, then the fraction with a smaller denominator is greater.
Read More:
- Conversion of Decimal into Fraction
- Operations on Fractions
- RS Aggarwal Class 6 Solutions Fractions
- RS Aggarwal Class 7 Solutions Fractions
2. Fraction with the same denominator
Let us consider the following fractions with the same denominator \(\frac{1}{8}\), \(\frac{3}{8}\), \(\frac{4}{8}\), \(\frac{7}{8}\)
The pictorial representation of these fractions are given below:
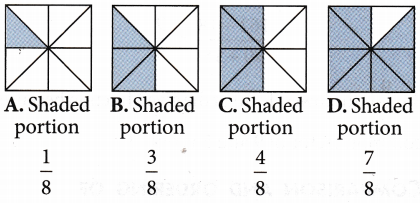
By looking at the shaded portion in these pictures, we can easily say that
shaded area of D > shaded area of C > shaded area of B > shaded area of A
\(\frac{7}{8}\) > \(\frac{4}{8}\) > \(\frac{3}{8}\) > \(\frac{1}{8}\)
Thus, we conclude that if two or more fractions have the same denominator, then the fraction with the greater numerator is the greater fraction.
3. Fractions with different numerators and denominators
To compare the fractions with different numerators and denominators, first we find the LCM of their denominators. Then, we make the denominator of each fraction equal to the LCM by multiplying with a suitable number.
Example 1: Compare the fractions \(\frac{3}{4}\), \(\frac{5}{6}\), \(\frac{6}{7}\), \(\frac{7}{8}\)
Solution: LCM of denominators 4,6,7, and 8 = 168
Hence, the given fractions can be written as
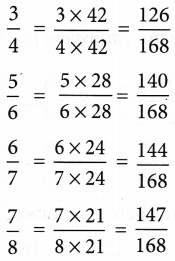
given fractions can be written as
Example 2: Arrange the following fractions in ascending order:
Solution: LCM of denominators 4,2,8, and 16
Hence, the given fractions can be written as
