Common Chord of Two Intersecting Circles
A line joining common points of two intersecting circles is called common chord.
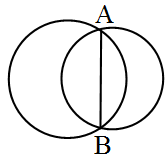 AB is common chord.
AB is common chord.
Read More:
- Parts of a Circle
- Perimeter of A Circle
- Construction of a Circle
- The Area of A Circle
- Properties of Circles
- Sector of A Circle
- The Area of A Segment of A Circle
- The Area of A Sector of A Circle
Common Chord of Two Intersecting Circles Example Problems with Solutions
Example 1: If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Solution:

IInd method
Let PC1C2 Q is a line. We will prove that line PQ is ⊥ bisector of common chord AB.
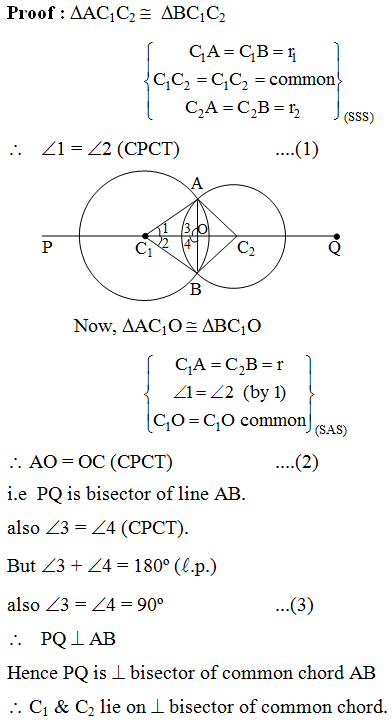
Example 2: If two intersecting chords of a circle make equal angles with the diameter passing through their point of intersection, prove that the chords are equal.
Solution: Given that AB and CD are two chords of a circle, with centre O intersecting at a point E. PQ is a diameter through E, such that ∠AEQ = ∠DEQ. We have to prove that AB = CD. Draw perpendiculars OL and OM on chords AB and CD, respectively. Now
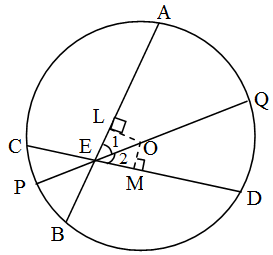

Example 3: Three girls Reshma, Salma and Mandeep are playing a game by standing on a circle of radius 5 m drawn in a pack. Reshma throws a ball to Salma, Salma to Mandeep. Mandeep to Reshma. If the distance between Reshma and Salma and between Salma and Mandeep is 6 m each. What is the distance between Reshma and Mandeep ?
Solution: Let the position of Reshma, Salma and Mandeep be at R, S and M on the circumference of the circular park.

Example 4: AB and CD are two parallel chords of a circle such that AB = 10 cm and CD = 24 cm. If the chords are on the opposite sides of the centre and the distance between them is 17 cm, find the radius of the circle.
Solution: let O be the centre of the given circle and let its radius be r cm. Draw OP ⊥ AB and OQ ⊥ CD. Since OP ⊥ AB, OQ ⊥ CD and AB || CD. Therefore, points P, O and Q are collinear. So, PQ = 17 cm.
Let OP = x cm. Then, OQ = (17 – x) cm.
Join OA and OC. Then, OA = OC = r.
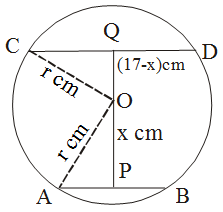 Since the perpendicular from the centre to a chord of the circle bisects the chord.
Since the perpendicular from the centre to a chord of the circle bisects the chord.

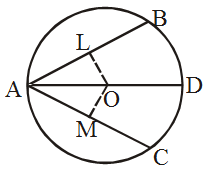
Example 5: If two chords of a circle are equally inclined to the diameter through their point of intersection, prove that the chords are equal.
Solution: Given. Two chords AB and AC of a circle C(O, r), such that AB and AC are equally inclined to diameter AOD.

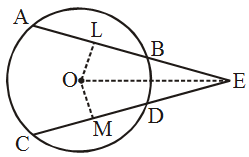
Example 6: Two equal chords AB and CD of a circle with centre O, when produced meet at a point E. Prove that BE = DE and AE = CE.
Solution: Given. Two equal chords AB and CD intersecting at a point E.
To prove. BE = DE and AE = CE.
Construction. Join OE, Draw OL ⊥ AB and OM ⊥ CD

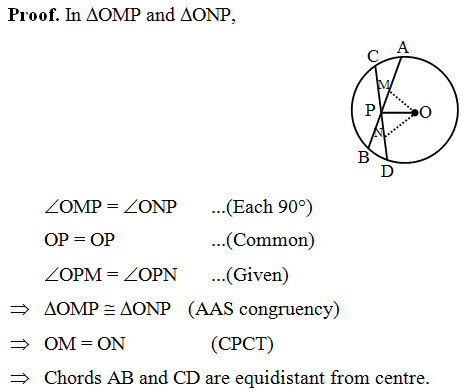
Example 7: O is the centre of the circle and PO bisects the angle APD. Prove that AB = CD.
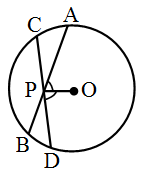 Solution: Given. A circle with centre O. Chords AB
Solution: Given. A circle with centre O. Chords AB
and CD meet at point P. PO bisects the angle APD.
To prove. AB = CD
Construction. Draw OM ⊥ AB and ON ⊥ CD.
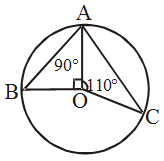
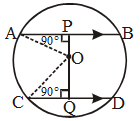
Example 8: O is the centre of the circle. If ∠BOA = 90° and ∠COA = 110°, find ∠BAC.
Solution: Given : A circle with centre O and
∠AOB = 90°, ∠AOC = 110°.
To find : ∠BAC = ?
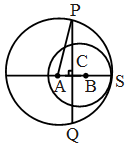
Example 9: Two circles with centres, A and B and of radii
5 cm and 3 cm respectively touch each other internally. If the perpendicular bisector of segment AB meets the bigger circle in P and Q. Find the length of PQ.
 Solution: Given. Two circles touch internally at S, A and B be the centres of the bigger and smaller circle respectively. The perpendicular bisector PQ bisects AB and meets the circle at P and Q.
Solution: Given. Two circles touch internally at S, A and B be the centres of the bigger and smaller circle respectively. The perpendicular bisector PQ bisects AB and meets the circle at P and Q.

Example 10: O is the centre of the circle with radius 5 cm. OP ⊥ AB, OQ ⊥ CD, AB || CD, AB = 8 cm and CD = 6 cm. Determine PQ.
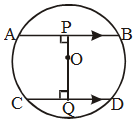 Solution: Given. AB and CD are two parallel chords.
Solution: Given. AB and CD are two parallel chords.
AB = 8 cm, CD = 6 cm, radius = 5 cm.
To find. PQ
Construction. Join OA, OC where O is the centre of the circle.

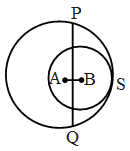
Example 11: If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, Prove that AB = CD (figure)
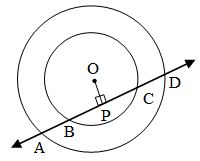 Solution:
Solution:

