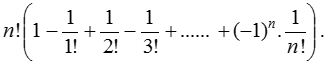What is Combination and What is the Formula for nCr?
Combinations
Definition:
Each of the different groups or selections which can be formed by taking some or all of a number of objects, irrespective of their arrangements, is called a combination.
Notation: The number of all combinations of n things, taken r at a time is denoted by
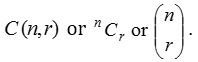
nCr is always a natural number.

Difference between a permutation and combination:
- In a combination only selection is made whereas in a permutation not only a selection is made but also an arrangement in a definite order is considered.
- Each combination corresponds to many permutations. For example, the six permutations ABC, ACB, BCA, BAC, CBA and CAB correspond to the same combination ABC.
Number of combinations without repetition
The number of combinations (selections or groups) that can be formed from n different objects taken r(0 ≤ r ≤ n) at a time is
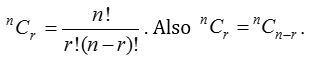
Let the total number of selections (or groups) = x. Each group contains r objects, which can be arranged in r ! ways. Hence the number of arrangements of r objects = x × (r!). But the number of arrangements = nPr.
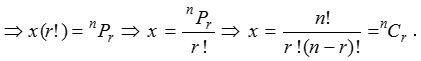
Number of combinations with repetition and all possible selections
- The number of combinations of n distinct objects taken r at a time when any object may be repeated any number of times.
= Coefficient of xr in (1 + x + x2 + …… + xr)n
= Coefficient of xr in (1 – x)–n = n + r – 1Cr - The total number of ways in which it is possible to form groups by taking some or all of n things at a time is
nC1 + nC2 + ……… + nCn = 2n – 1. - The total number of ways in which it is possible to make groups by taking some or all out of n = (n1 + n2 + ….) things, when n1 are alike of one kind, n2 are alike of second kind, and so on is {(n1 + 1)(n2 + 1)…..} – 1.
- The number of selections of r objects out of n identical objects is 1.
- Total number of selections of zero or more objects from n identical objects is n + 1.
- The number of selections taking at least one out of a1 + a2 + a3 + …… + an + k objects, where a1 are alike (of one kind), a2 are alike (of second kind) and so on…… an are alike (of nth kind) and k are distinct = [(a1 + 1)(a2 + 1)(a3 + 1) ……….. (an + 1)]2k – 1.
Conditional combinations
(1) The number of ways in which r objects can be selected from n different objects if k particular objects are
- Always included = n–kCr–k
- Never included = n–kCr
(2) The number of combinations of n objects, of which p are identical, taken r at a time is
n–pCr + n–pCr–1 + n–pCr–2 + ……… + n–pC0, if r ≤ p and
n–pCr + n–pCr–1 + n–pCr–2 + ……… + n–pCr–p, if r > p.
Division into groups
Case I :
- The number of ways in which n different things can be arranged into r different groups is n + r – 1Pn or n! n–1Cr–1 according as blank group are or are not admissible.
- The number of ways in which n different things can be distributed into r different group is
rn – rC1(r – 1)n + rC2(r – 2)n – ………. + (–1)n–1 nCr–1 or Coefficient of xn is n ! (ex – 1)r.
Here blank groups are not allowed. - Number of ways in which m × n different objects can be distributed equally among n persons (or numbered groups) = (number of ways of dividing into groups) × (number of groups) ! =
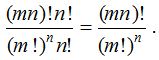
Case II :
(1) The number of ways in which different things can be divided into two groups which contain m and n things respectively is,
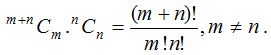
Corollary: If m = n, then the groups are equal size. Division of these groups can be given by two types.
Type I : If order of group is not important : The number of ways in which 2n different things can be divided equally into two groups is
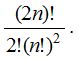
Type II : If order of group is important : The number of ways in which 2n different things can be divided equally into two distinct groups is
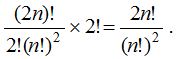
(2) The number of ways in which (m + n + p) different things can be divided into three groups which contain m, n and p things respectively is
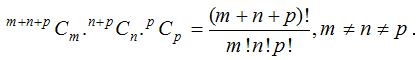
Corollary : If m = n = p, then the groups are equal size. Division of these groups can be given by two types.
Type I : If order of group is not important : The number of ways in which 3p different things can be divided equally into three groups is
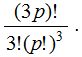
Type II : If order of group is important : The number of ways in which 3p different things can be divided equally into three distinct groups is
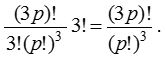
(i) If order of group is not important : The number of ways in which mn different things can be divided equally into m groups is
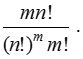
(ii) If order of group is important: The number of ways in which mn different things can be divided equally into m distinct groups is
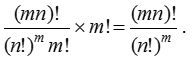
Derangement
Any change in the given order of the things is called a derangement.
If n things form an arrangement in a row, the number of ways in which they can be deranged so that no one of them occupies its original place is