Classification of Triangles
A triangle is a polygon with three sides. It has three sides and three vertices. There are seven types of triangles. The sum of the angles of a triangle is 180°.
Triangles Types can be classified in two ways:
- By their sides
- By their angles
what are the six types of triangles?
Six Various Types of Triangles are Isosceles, Equilateral, Obtuse, Acute and Scalene.
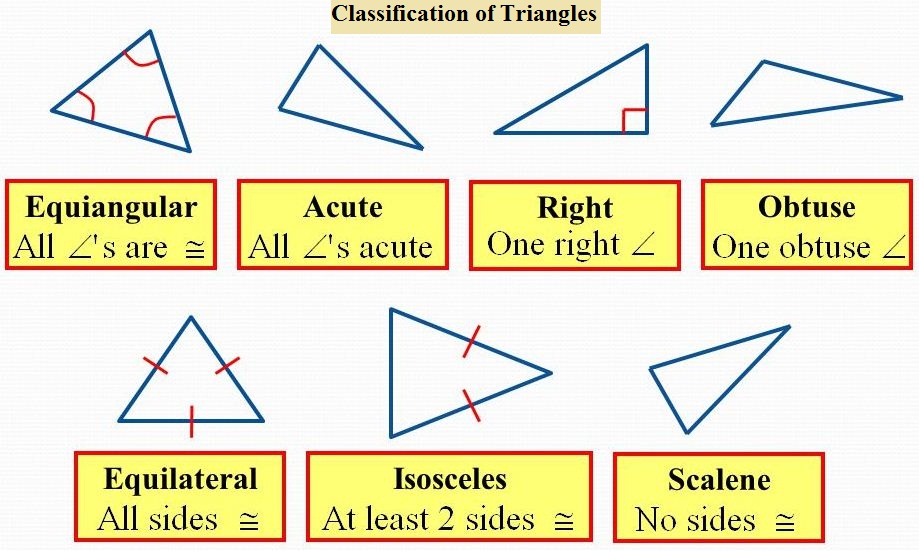
Classification of Triangles by Sides
Scalene Triangle:
A triangle that has no side of equal length is called a scalene triangle.
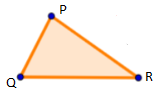 In figure, PQ ≠ QR ≠ PR, so ΔPQR is a scalene triangle.
In figure, PQ ≠ QR ≠ PR, so ΔPQR is a scalene triangle.
Isosceles Triangle:
A triangle that has two sides of equal length, is called an isosceles triangle.
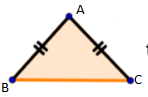 In figure, AB = AC, so ΔABC is an isosceles triangle.
In figure, AB = AC, so ΔABC is an isosceles triangle.
Equilateral Triangle:
A triangle which has all the three sides equal in length is called an equilateral triangle.
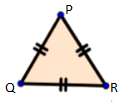 In figure, PQ = QR = PR, so ΔPQR is an equilateral triangle.
In figure, PQ = QR = PR, so ΔPQR is an equilateral triangle.
Classification of Triangles by Angles
Acute-angled Triangle:
A triangle whose all angles are acute (less than 90°), is called an acute-angled triangle or simply an acute triangle.
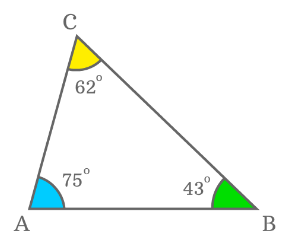 In figure, ∠A, ∠B, and ∠C are all less than 90°, hence ΔABC is an acute-angled triangle.
In figure, ∠A, ∠B, and ∠C are all less than 90°, hence ΔABC is an acute-angled triangle.
Right-angled Triangle:
A triangle whose one of the angles is a right angle, i.e., 90°, is called a right-angled triangle or simply right triangle.
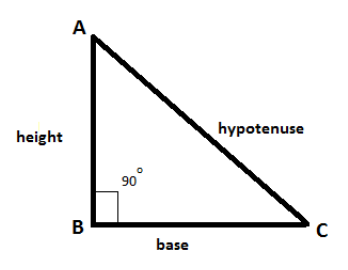 In figure, ∠B = 90°, hence ΔABC is a right triangle.
In figure, ∠B = 90°, hence ΔABC is a right triangle.
Obtuse-angled Triangle:
A triangle whose one angle is obtuse, is called an obtuse-angled triangle or simply obtuse triangle.
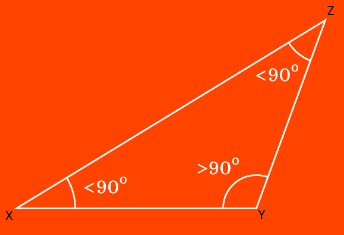 In figure, ∠Y is obtuse, hence ΔXYZ is an obtuse-angled triangle or simply obtuse triangle.
In figure, ∠Y is obtuse, hence ΔXYZ is an obtuse-angled triangle or simply obtuse triangle.
Equiangular Triangle:
When all the three angles of a triangle are equal, then it is known as an equiangular triangle.
An equiangular triangle is also known as equilateral triangle because all the three sides are equal.
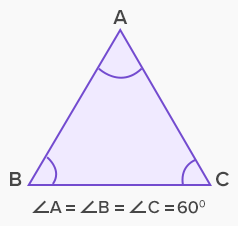 In figure, ∠A = ∠B = ∠C = 60°and AB = BC = AC, hence ΔABC is an equiangular triangle.
In figure, ∠A = ∠B = ∠C = 60°and AB = BC = AC, hence ΔABC is an equiangular triangle.
Example 1: One of the equal angles of an isosceles triangle is 50°. Find its third angle.
Solution: Let third angle = x
∴ x + 50° + 50° = 180°
(Angle sum property of a triangle)
or, x + 100° = 180°
or, x = 180° – 100°
= 80°
∴ Third angle = 80°
Example 2: Each ofthe two equal angles of a triangle is four times the third angle. Find all the angles of the triangle.
Solution: Let the smaller angle = x
∴ other two angles = 4x and 4x
Thus, x + 4x + 4x = 180°
(Angle sum property of a triangle) or, 9x = 180°
∴ 4x = 4 x 20°
= 80°
Thus, the angles of the triangle are 20°, 80°, and 80°.
Read More:
- Angle Sum Property of a Triangle
- Median and Altitude of a Triangle
- The Angle of An Isosceles Triangle
- Areas of Two Similar Triangles
- Proofs with Similar Triangles
- Criteria For Similarity of Triangles
- Area of A Triangle
- Areas of an Isosceles Triangle and an Equilateral Triangle
- Construction of an Equilateral Triangle
- How Do You Prove Triangles Are Congruent
- Criteria For Congruent Triangles
