ICSE Solutions for Class 10 Mathematics - Circles

ICSE Solutions for Class 10 Mathematics – Circles

ICSE SolutionsSelina ICSE Solutions

Get ICSE Solutions for Class 10 Mathematics Chapter 15 Circles for ICSE Board Examinations on APlusTopper.com. We provide step by step Solutions for ICSE Mathematics Class 10 Solutions Pdf. You can download the Class 10 Maths ICSE Textbook Solutions with Free PDF download option.

Download Formulae Handbook For ICSE Class 9 and 10

Formulae

Theorems based on chord properties:

1. Theorem: A straight line drawn from the centre of the circle to bisect a chord, which is not a diameter, is at right angles to the chord.
   Conversely, the perpendicular to a chord, from the centre of the circle, bisects the chord.
2. Theorem: There is one circle, and only one, which passes through three given points not in a straight line.
3. Theorem: Equal chords of a circle are equidistant from the centre.
   Conversely, chords of a circle, equidistant from the centre of the circle, are equal.
   

Theorems based on Arc and Chord properties:

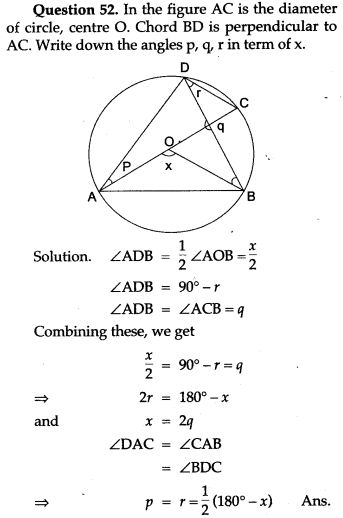
1. Theorem: The angle which an arc of a circle subtends at the centre is double, that which it subtends at any point on the remaining part of the circumference.
2. Theorem: Angles in the same segment of a circle are equal.
3. Theorem: The angle in a semicircle is a right angle.
4. Theorem: In equal circles (or, in the same circle), if two arcs subtends equal angles at the centre, they are equal.
   Conversely, in equal circles (or, in the same circle), if two arcs are equal, they subtend equal angles at the centre.
5. Theorem: In equal circles (or, in the same circle), if two chord are equal, they cut off equal arcs.
   Conversely, in equal circles (or, in the same circle, if two arcs are equal the chords of the arcs are also equal.

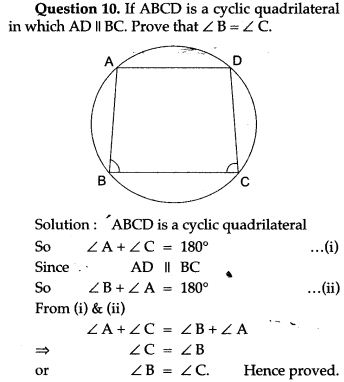
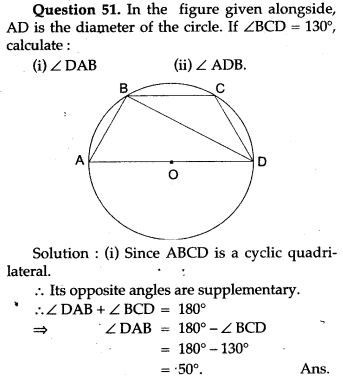
Theorems based on Cyclic properties: ABCD is a cyclic quadrilateral.

1. Theorem: The opposite angles of a cyclic quadrilateral (quadrilateral inscribed in a circle) are supplementary.
2. Theorem: The exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.

Theorems based on Tangent Properties:

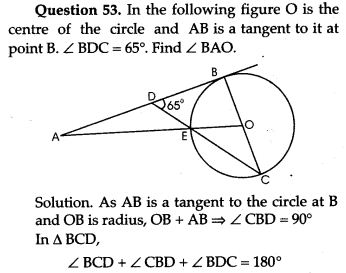
1. Theorem: The tangent at any point of a circle and the radius through this point are perpendicular to each other.
2. Theorem: If two circles touch each other, the point of contact lies on the straight line through the centres.
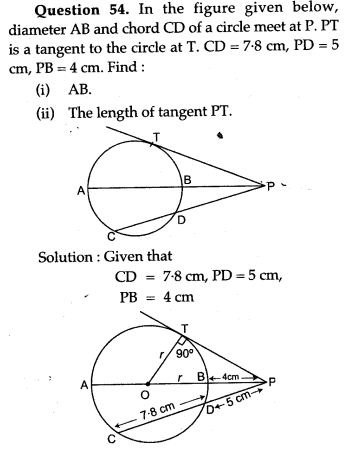
3. Theorem: From any point outside a circle two tangents can be drawn and they are equal in length.
4. Theorem: If a chord and a tangent intersect externally, then the product of the lengths of segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.
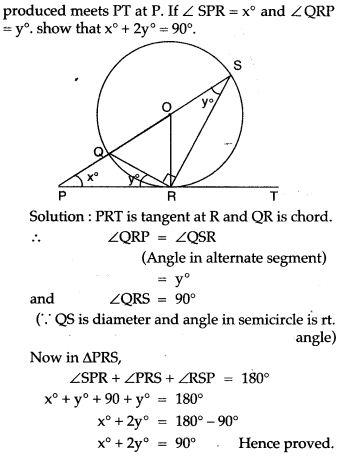
5. Theorem: If a line touches a circle and from the point of contact, a chord is drawn, the angles between the tangent and the chord are respectively equal to the angles in the corresponding alternate segments.

Prove the Following 

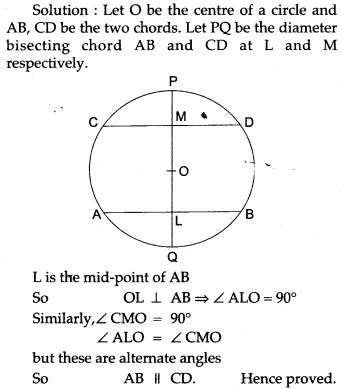
Question 1. If a diameter of a circle bisect each of the two chords of a circle, prove that the chords are parallel.

Question 2. If two chords of a circle are equally inclined to the diameter through their point of intersection, prove that the chords are equal.

Question 3. In the given figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA = 2 OD.

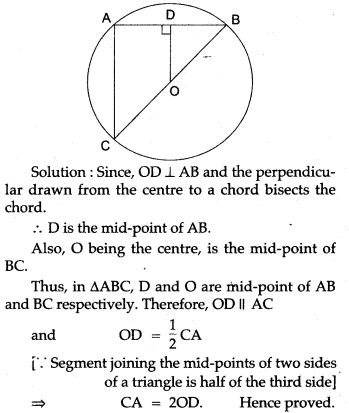
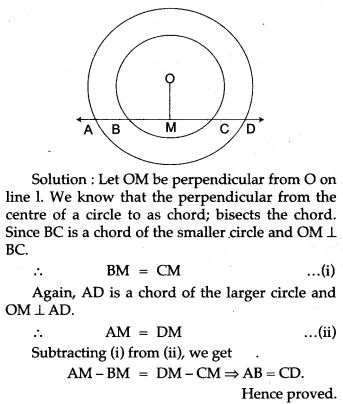
Question 4. In Fig., l is a line intersecting the two concentric circles, whose common centre is O, at the points A, B, C and D. Show that AB = CD.

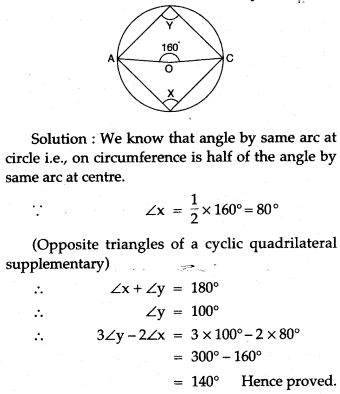
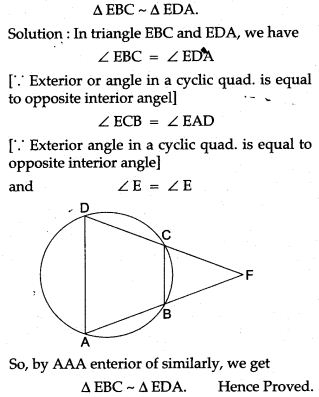
Question 6. ABCD is a cyclic quadrilateral AB and DC are produced to meet in E. Prove that

Question 7. In an isosceles triangle ABC with AB = AC, a circle passing through B and C intersects the sides. AB, and AC at D and E respectively. Prove that DE || BC.

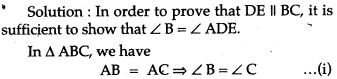
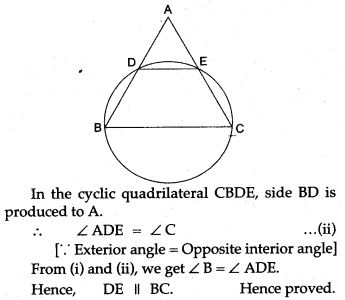
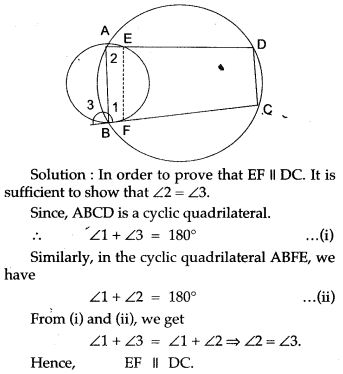
Question 8. ABCD is quadrilateral inscribed in circle, having ∠A = 60°, O is the centre of the circle, show that

Question 9. Two equal circles intersect in P and Q. A straight line through P meets the circles in A and B. Prove that QA = QB

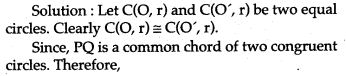
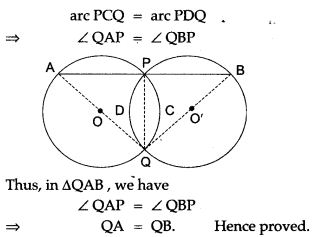
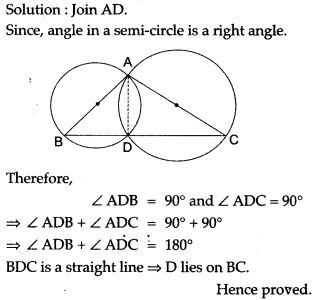
Question 11. Two circles are drawn with sides AB, AC of a triangle ABC as diameters. The circles intersect at a point D. Prove that D lies on BC.

Question 12. In the given figure, PT touches a circle with centre O at R. Diameter SQ when

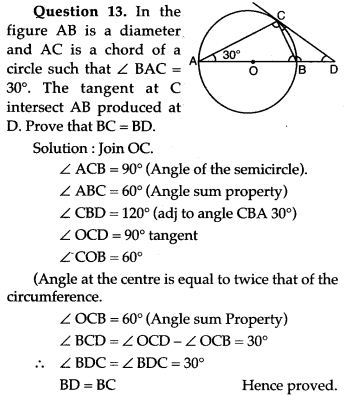
Question 14. Prove that the line segment joining the midpoints of two equal chords of a circle substends equal angles with the chord.

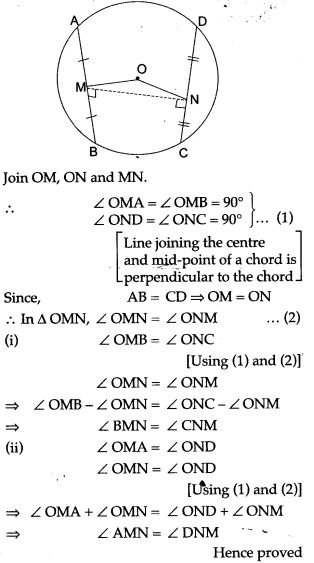
Question 15. In an equilateral triangle, prove that the centroid and centre of the circum-circle (circumcentre) coincide.


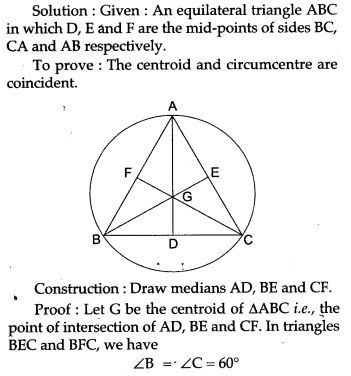
Question 16. In Fig. AB and CD are two chords of a circle intersecting each other at P such that AP = CP. Show that AB = CD.

Question 17. Prove that the angle bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (Provided they are not parallel) intersect at right angle.

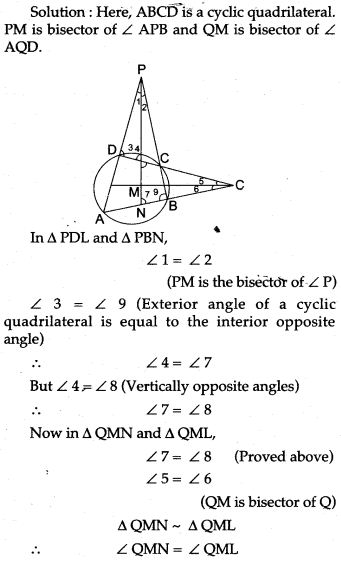
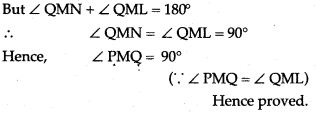
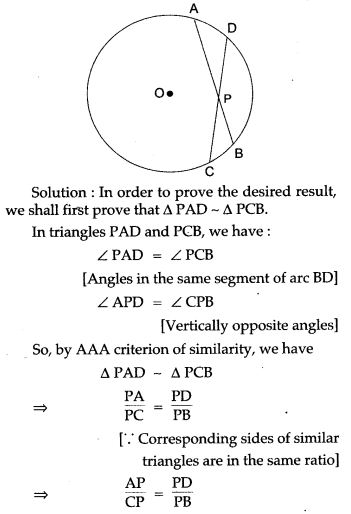
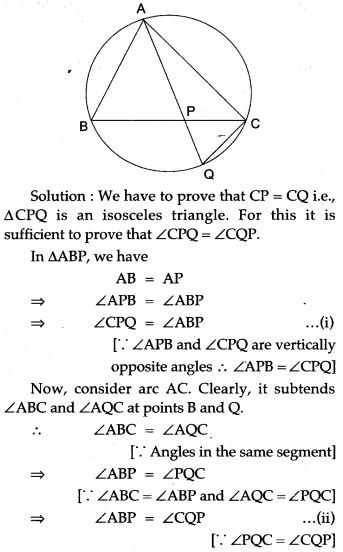
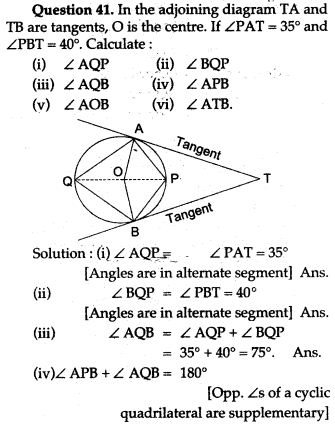
Question 18. In Fig. P is any point on the chord BC of a circle such that AB = AP. Prove that CP = CQ.

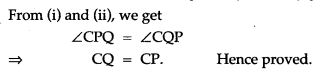
Question 19. The diagonals of a cyclic quadrilateral are at right angles. Prove that the perpendicular from the point of their intersection on any side when produced backward bisects the opposite side.

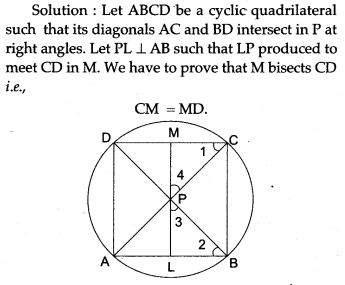
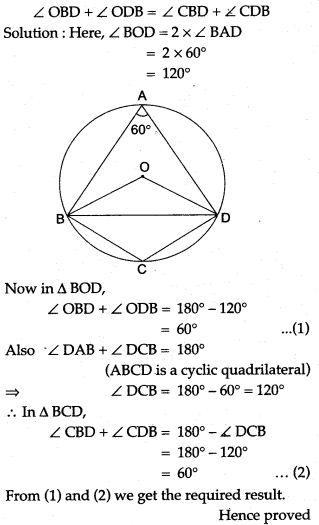
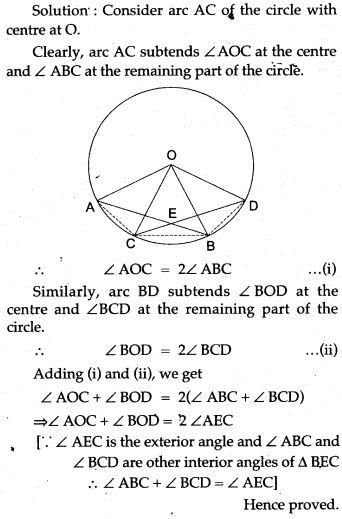
Question 20. In a circle with centre O, chords AB and CD intersect inside the circumference at E. Prove that ∠AOC + ∠BOD = 2∠AEC.

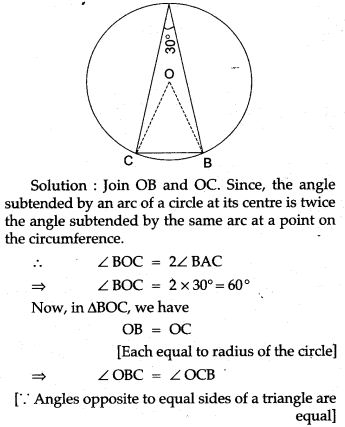
Question 21. In Fig. ABC is a triangle in which ∠BAC = 30°. Show that BC is the radius of the circum circle of A ABC, whose centre is O.

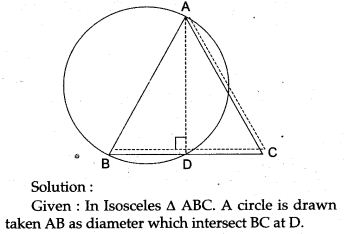
Question 22. Prove that the circle drawn on any one of the equal sides of an isosceles triangles as diameter bisects the base.

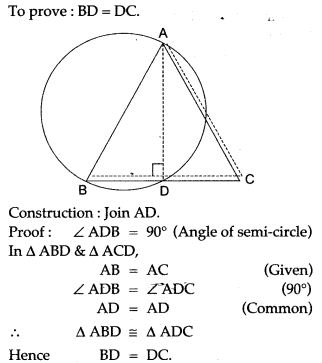
Question 23. In Fig. ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EF || DC.

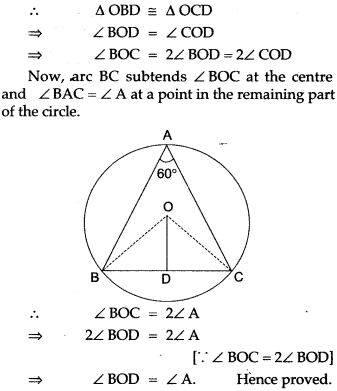
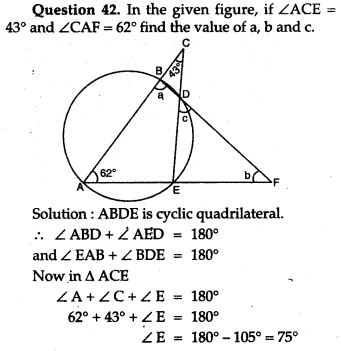
Question 25. If PA and PB are two tangent drawn from a point P to a circle with centre C touching it A and B, prove that CP is the perpendicular bisector of AB.

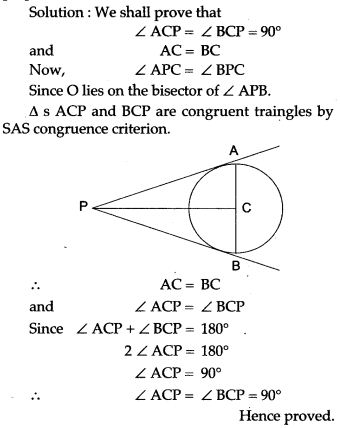
Question 26. Two circle with radii r₁ and r₂ touch each other externally. Let r be the radius of a circle which touches these two circle as well as a common tangent to the two circles, Prove that:

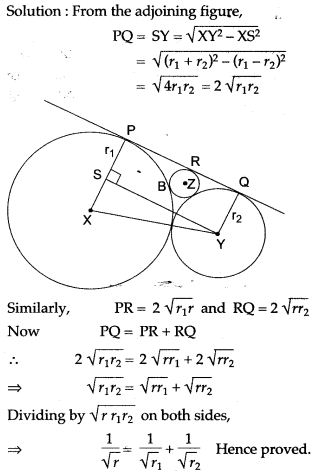
Question 27. If AB and CD are two chords which when produced meet at P and if AP = CP, show that AB = CD.

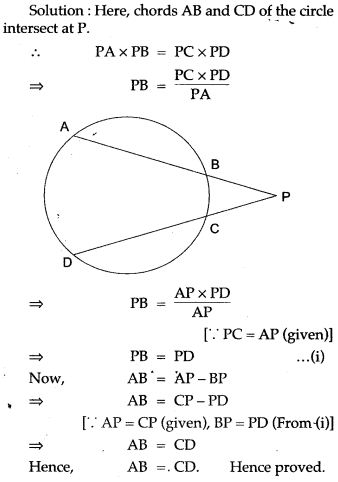
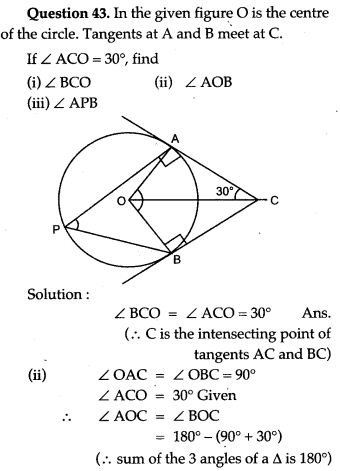
Question 28. In the figure, PM is a tangent to the circle and PA = AM. Prove that:

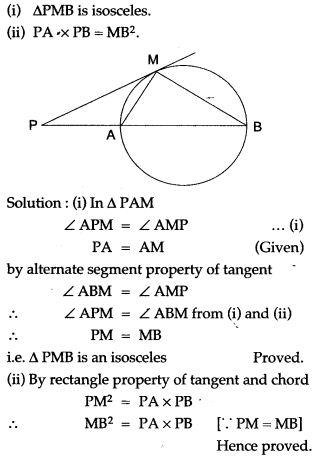
Question 29. In Fig. the incircle of ΔABC, touches the sides BC, CA and AB at D, E respectively. Show that:

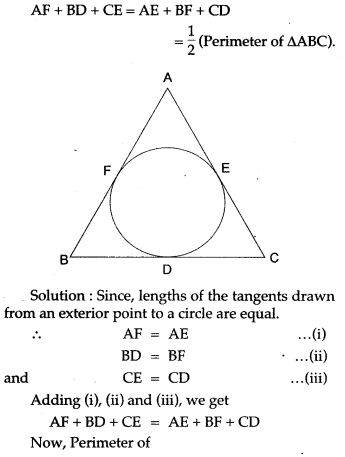
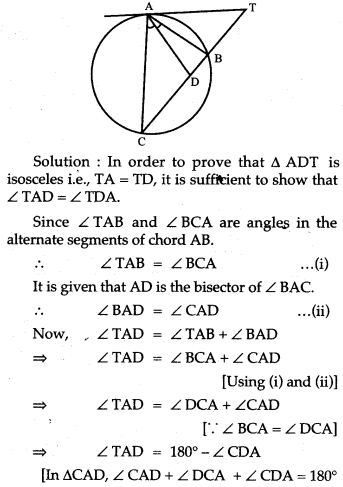
Question 30. In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

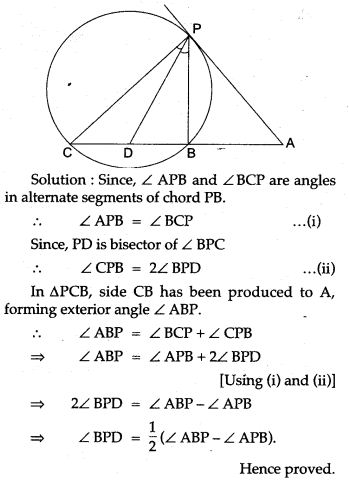
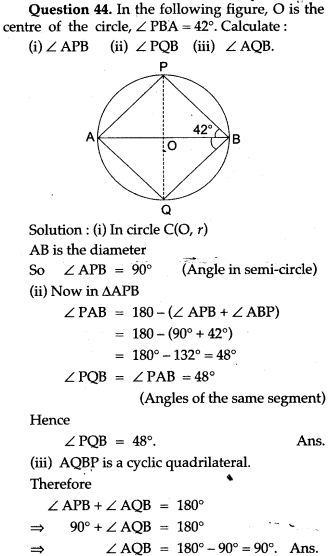
Question 32. In Fig. l and m are two parallel tangents at A and B. The tangent at C makes an intercept DE between n and m. Prove that ∠ DFE = 90⁰

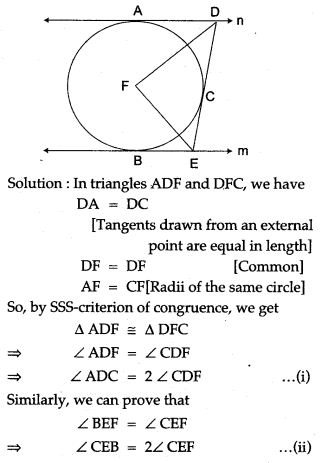
Question 33. A circle touches the sides of a quadrilateral ABCD at P, Q, R, S respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.

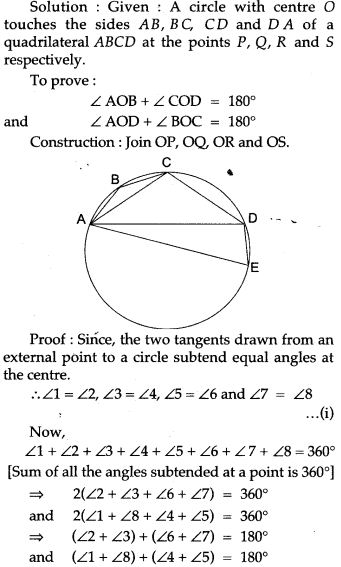
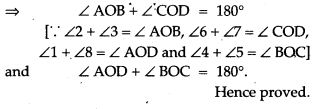
Question 34. Two equal chords AB and CD of a circle with centre O, when produced meet at a point E, as shown in Fig. Prove that BE = DE and AE = CE.

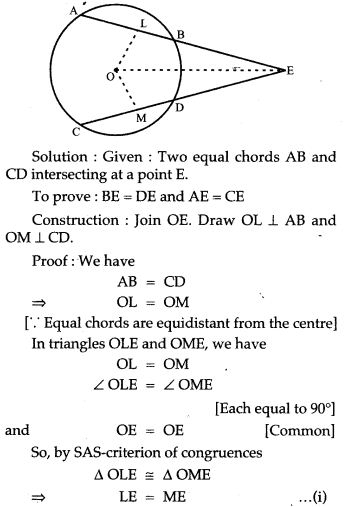
Question 35. Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.

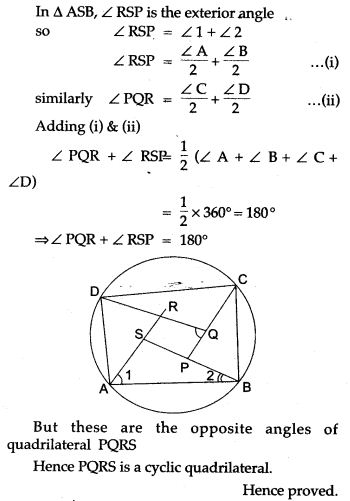
Figure Based Questions

Question 1. Two concentric circles with centre 0 have A, B, C, D as the points of intersection with the lines L shown in figure. If AD = 12 cm and BC s = 8 cm, find the lengths of AB, CD, AC and BD.

Question 2. In the given circle with diameter AB, find the value of x.

Question 3. In the given figure, the area enclosed between the two concentric circles is 770 cm². If the radius of outer circle is 21 cm, calculate the radius of the inner circle.

Question 4. Two chords AB and CD of a circle are parallel and a line L is the perpendicular bisector of AB. Show that L bisects CD.

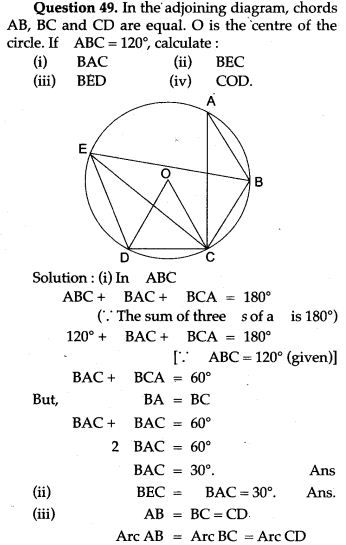
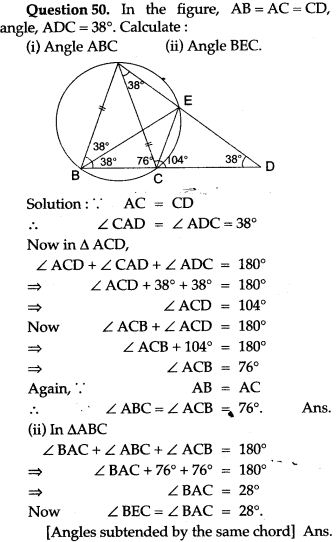
Question 5. In the adjoining figure, AB is the diameter of the circle with centre O. If ∠BCD = 120°, calculate:

Question 6. Find the length of a chord which is at a distance of 5 cm from the centre of a circle of radius 13 cm.

Question 7. The radius of a circle is 13 cm and the length of one of its chord is 10 cm. Find the distance of the chord from the centre.

Question 9. AB is a diameter of a circle with centre C = (- 2, 5). If A = (3, – 7). Find
(i) the length of radius AC
(ii) the coordinates of B.

Question 10. AB is a diameter of a circle with centre O and radius OD is perpendicular to AB. If C is any point on arc DB, find ∠ BAD and ∠ ACD.

Question 11. In the given below figure,

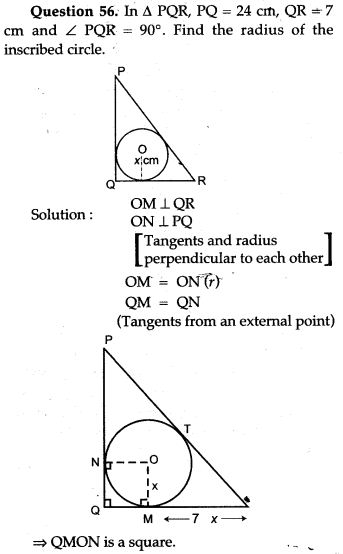
Question 14. In the given figure O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of the circle.

Question 15. In Fig., chords AB and CD of the circle intersect at O. AO = 5 cm, BO = 3 cm and CO = 2.5 cm. Determine the length of DO.

Question 16. In the figure given below, PT is a tangent to the circle. Find PT if AT = 16 cm and AB = 12 cm.

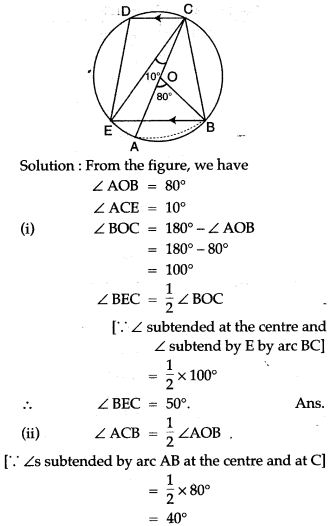
Question 18. A, B and C are three points on a circle. The tangent at C meets BN produced at T. Given that ∠ ATC = 36° and ∠ ACT = 48°, calculate the angle subtended by AB at the centre of the circle.

Question 19. In the given figure, O is the centre of the circle and ∠PBA = 45°. Calculate the value of ∠PQB.

Question 20. Two chords AB, CD of lengths 16 cm and 30 cm, are parallel. If the distance between AB and CD is 23 cm. Find the radius of the circle.

Question 21. Two circles of radii 10 cm and 8 cm intersect and the length of the common chord is 12 cm. Find the distance between their centres.

Question 22. AB and CD are two chords of a circle such that AB = 6 cm, CD = 12 cm and AB || CD. If the distance between AB and CD is 3 cm, find the radius of the circle.

Question 24. AB and CD are two parallel chords of a circle such that AB = 10 cm and CD = 24 cm. If the chords are on the opposite sides of the centre and the distance between them is 17 cm, find the radius of the circle.

Question 26. In the figure given below,O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD.

Question 27. If O is the centre of the circle, find the value of x in each of the following figures

Question 29. In the given figure, AB is the diameter of a circle with centre O.

Question 30. In ABCD is a cyclic quadrilateral; O is the centre of the circle. If BOD = 160°, find the measure of BPD.

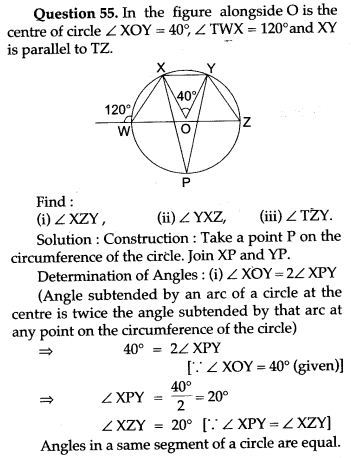
Question 32. In the given figure O is the centre of the circle, ∠ BAD = 75° and chord BC = chord CD. Find:

Question 37. ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

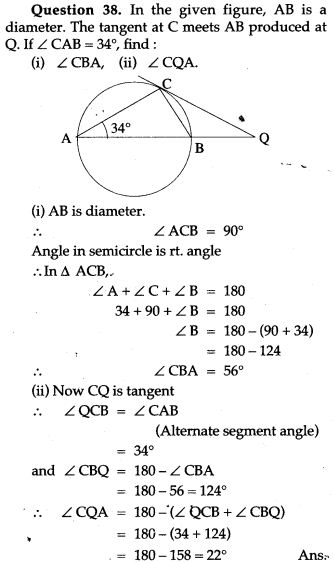
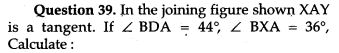
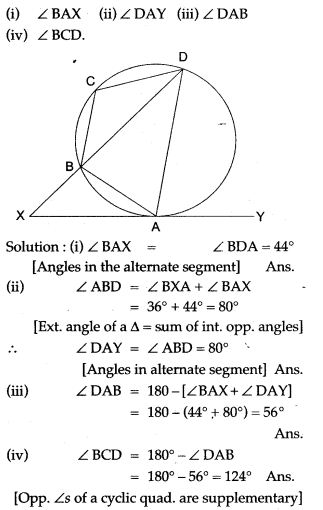
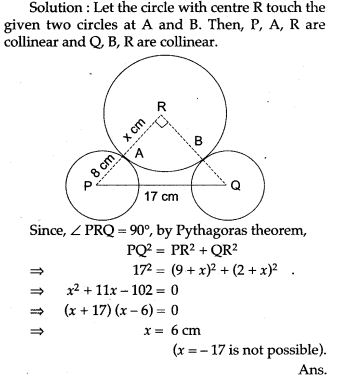
Question 40. P and Q are the centre of circles of radius 9 cm and 2 cm respectively; PQ = 17 cm. R is the centre of circle of radius x cm, which touches the above circles externally, given that ∠ PRQ = 90°. Write an equation in x and solve it.

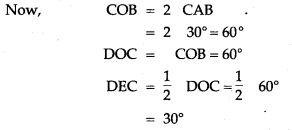
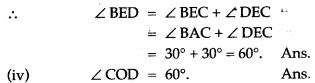
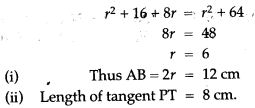
For More Resources