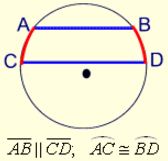
Circles and Chords
A chord is a segment that joins two points of the circle.
A diameter is a chord that contains the center of the circle.
Theorems:
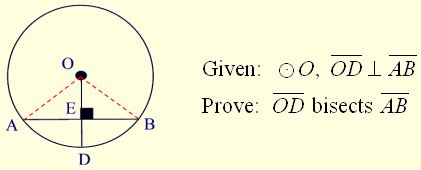
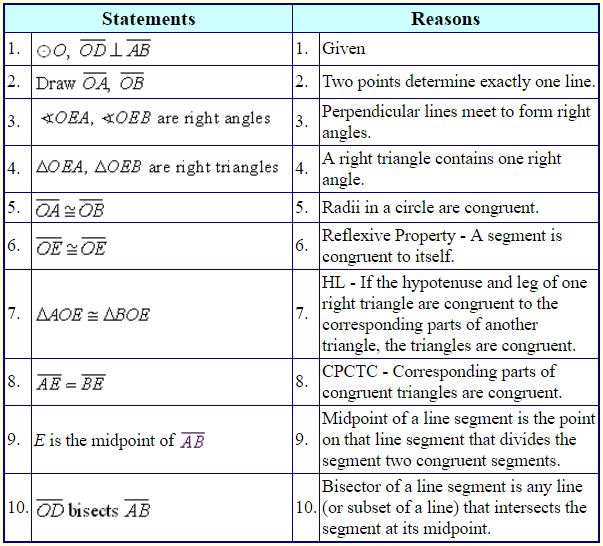
- In a circle, a radius perpendicular to a chord bisects the chord.
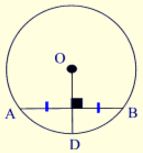
- In a circle, a radius that bisects a chord is perpendicular to the chord.
- In a circle, the perpendicular bisector of a chord passes through the center of the circle.
Proof of Theorem 1:
Theorem:
In a circle, or congruent circles, congruent chords are equidistant from the center.
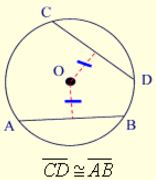 (converse) In a circle, or congruent circles, chords equidistant from the center are congruent.
(converse) In a circle, or congruent circles, chords equidistant from the center are congruent.
Theorem:
In a circle, or congruent circles, congruent chords have congruent arcs.
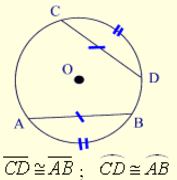 (converse) In a circle, or congruent circles, congruent arcs have congruent chords.
(converse) In a circle, or congruent circles, congruent arcs have congruent chords.
Theorem:
In a circle, parallel chords intercept congruent arcs.