Circle Equations
A circle is defined as the locus of a point which moves in a plane such that its distance from a fixed point in that plane always remains the same i.e., constant.
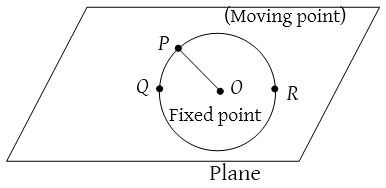 The fixed point is called the centre of the circle and the fixed distance is called the radius of the circle.
The fixed point is called the centre of the circle and the fixed distance is called the radius of the circle.
Standard forms of equation of a circle
General equation of a circle:
The general equation of a circle is x2 + y2 + 2gx + 2fy + c = 0 where g, f, c are constant.
- Centre of the circle is (–g, –f). i.e., (–1/2 coefficient of x, –1/2 coefficient of y).
- Radius of the circle is \(\sqrt { { g }^{ 2 }+{ f }^{ 2 }-c }\).
Nature of the circle:
- If g2 + f2 − c > 0, then the radius of the circle will be real. Hence, in this case, it is possible to draw a circle on a plane.
- If g2 + f2 − c = 0, then the radius of the circle will be zero. Such a circle is known as point circle.
- If g2 + f2 − c < 0, then the radius \(\sqrt { { g }^{ 2 }+{ f }^{ 2 }-c }\) of the circle will be an imaginary number. Hence, in this case, it is not possible to draw a circle.
The condition for the second degree equation to represent a circle:
The general equation represents a circle iff
- a = b ≠ 0
- h = 0
- ∆ = abc + 2hgf – af2 – bg2 – ch2 ≠ 0
- g2 + f2 – ac ≥ 0
Central form of equation of a circle:
The equation of a circle having centre (h, k) and radius r is (x – h)2 + (y – k)2 = r2
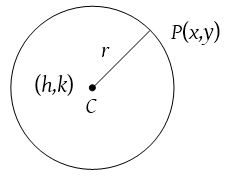 If the centre is origin, then the equation of the circle is x2 + y2 = r2
If the centre is origin, then the equation of the circle is x2 + y2 = r2
Circle on a given diameter:
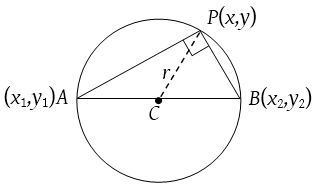
The equation of the circle drawn on the straight line joining two given points (x1, y1) and (x2, y2) as diameter is (x – x1)(x – x2) + (y – y1)(y – y2) = 0.
Parametric co-ordinates:
(i) The parametric co-ordinates of any point on the circle (x – h)2 + (y – k)2 = r2 are given by (h + r cos θ, k + r sin θ), (0 ≤ θ < 2π).
In particular, co-ordinates of any point on the circle x2 + y2 = r2 are (r cos θ, r sin θ), (0 ≤ θ < 2π).
(ii) The parametric co-ordinates of any point on the circle x2 + y2 + 2gx + 2fy + c = 0 are x = -g + \(\sqrt { { g }^{ 2 }+{ f }^{ 2 }-c }\) cos θ and y = -f + \(\sqrt { { g }^{ 2 }+{ f }^{ 2 }-c }\) sin θ, (0 ≤ θ < 2π) ,
(5) Equation of a circle under given conditions
(i) The equation of the circle through three non-collinear points is
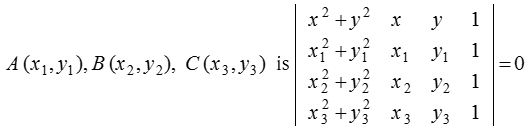 (ii) From given three points taking any two as extremities of diameter of a circle S = 0 and equation of straight line passing through these two points is L = 0. Then required equation of circle is S + λL = 0, where λ is a parameter, which can be found out by putting third point in the equation.
(ii) From given three points taking any two as extremities of diameter of a circle S = 0 and equation of straight line passing through these two points is L = 0. Then required equation of circle is S + λL = 0, where λ is a parameter, which can be found out by putting third point in the equation.
Equation of a circle in some special cases
(1) If centre of the circle is (h, k) and it passes through origin then its equation is (x – h)2 + (y – k)2 = h2 + k2 ⇒ x2 + y2 – 2hx – 2ky = 0.
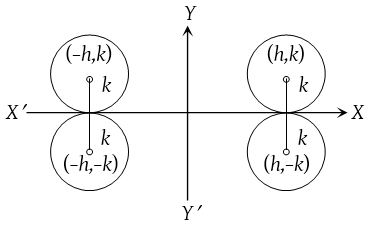
(2) If the circle touches x-axis then its equation is (x ± h)2 + (y ± k)2 = k2. (Four cases)
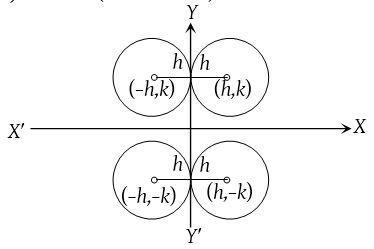
 (3) If the circle touches y-axis then its equation is (x ± h)2 + (y ± k)2 = h2. (Four cases)
(3) If the circle touches y-axis then its equation is (x ± h)2 + (y ± k)2 = h2. (Four cases)
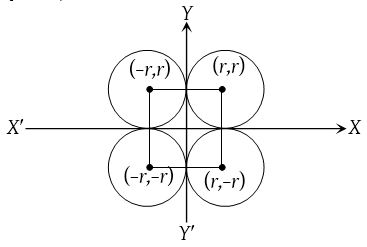
 (4) If the circle touches both the axes then its equation is (x ± r)2 + (y ± r)2 = r2. (Four cases)
(4) If the circle touches both the axes then its equation is (x ± r)2 + (y ± r)2 = r2. (Four cases)
 (5) If the circle touches x- axis at origin then its equation is x2 + (y ± k)2 = k2 ⇒ x2 + y2 ± 2ky = 0. (Two cases)
(5) If the circle touches x- axis at origin then its equation is x2 + (y ± k)2 = k2 ⇒ x2 + y2 ± 2ky = 0. (Two cases)
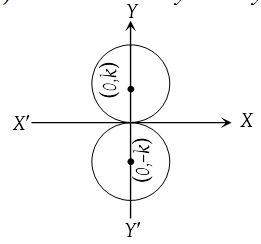 (6) If the circle touches y-axis at origin, the equation of circle is (x ± h)2 + y2 = h2 ⇒ x2 + y2 ± 2xh = 0. (Two cases)
(6) If the circle touches y-axis at origin, the equation of circle is (x ± h)2 + y2 = h2 ⇒ x2 + y2 ± 2xh = 0. (Two cases)
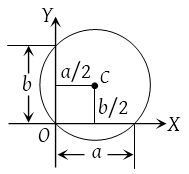
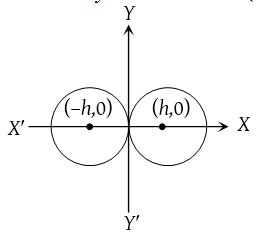 (7) If the circle passes through origin and cut intercepts a and b on axes, the equation of circle is and centre is x2 + y2 – ax – by = 0. (Four cases)
(7) If the circle passes through origin and cut intercepts a and b on axes, the equation of circle is and centre is x2 + y2 – ax – by = 0. (Four cases)