CBSE Sample Papers for Class 12 Maths Paper 7 are part of CBSE Sample Papers for Class 12 Maths. Here we have given CBSE Sample Papers for Class 12 Maths Paper 7.
CBSE Sample Papers for Class 12 Maths Paper 7
| Board | CBSE |
| Class | XII |
| Subject | Maths |
| Sample Paper Set | Paper 7 |
| Category | CBSE Sample Papers |
Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 7 of Solved CBSE Sample Paper for Class 12 Maths is given below with free PDF download solutions.
Time: 3 Hours
Maximum Marks: 100
General Instructions:
- All questions are compulsory.
- Questions 1-4 in section A are very short answer type questions carrying 1 mark each.
- Questions 5-12 in section B are short answer type questions carrying 2 marks each.
- Questions 13-23 in section C are long answer I type questions carrying 4 marks each.
- Questions 24-29 in section D are long answer II type questions carrying 6 marks each.
SECTION A
Question 1.
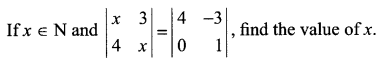
Question 2.
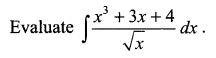
Question 3.
Find the slope of the tangent to the curve y = 3x4 – 4x at x = 4.
Question 4.
Find the direction cosines of the normal to the plane 2x + 3y – z = 5.1
SECTION B
Question 5.
Find the integral value of x if
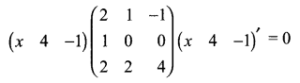
Question 6.
If xy = yx, find \(\frac { dy }{ dx }\)
Question 7.
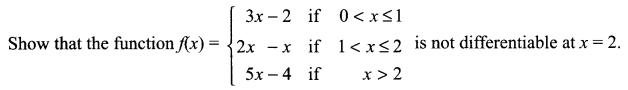
Question 8.
Water is running out of a conical funnel at the rate of 15 cm3/sec. If the radius of the base of funnel is 10 cm and altitude is 20 cm, find the rate at which water level is dropping when it is 10 cm from the top.
Question 9.
If \(\vec { a }\) and \(\vec { b }\) are unit vectors then what is the angle between \(\vec { a }\) and \(\vec { b }\) for √3 \(\vec { a }\) – \(\vec { b }\) to be a unit vector.
Question 10.
Find P(E|F): Mother, father and son line up at random for a family picture. E: son on one end, F: father in middle.
Question 11.
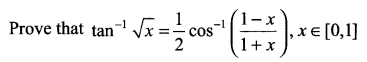
Question 12.
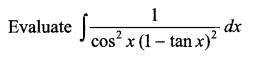
SECTION C
Question 13.
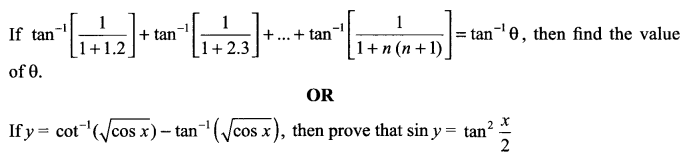
Question 14.

Question 15.
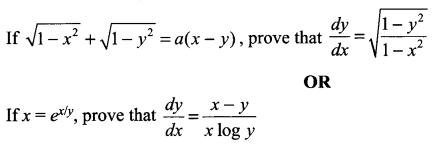
Question 16.
Question 17.
Question 18.
Solve the differential equation \(\frac { xdy }{ dx }\) = y (log y – log x + 1)
Question 19.
Find the equation of the line passing through the point (9, -1, 7) and perpendicular to the lines joining the points (4, 3, 2), (1, -1, 0) and (1, 2, -1), (2, 1, 1).
Question 20.
Question 21.
An anti-aircraft gun can take a maximum of 4 shots at an enemy plane moving away from it. The probability of hitting the plane at the first, second, third and fourth shot are 0.4, 0.3, 0.2, and 0.1 respectively. What is the probability that the gun hits the plane?
Question 22.
70% men and 30% women eat pan masala, 10% of these men and 20% of women eat X brand. What is the probability that a person seen eating X brand will be a man? Why do you discourage your friend to eat pan masala?
Question 23.
Let N be the set of all natural numbers and let R be a relation in N x N defined by
(a, b) R (c, d) ⇔ ad = bc
For all (a, b), (c, d) ∈ N x N. Show that R is an equivalence relation on N x N.
SECTION D
Question 24.
The management committee of a residential colony decided to award some of its members (say x) for honesty, some (say y) for helping or co-operating others and some (say z) for supervising the workers to keep the colony neat and clean. The sum of all the awardees are 12. Three times the sum of awardees for co-operation and supervision added to two times the number of awardees for honesty is 33. If the sum of the number of awardees for honesty and supervision is twice the number of awardees for helping others. Using matrix method, find the number of awardees of each category.
OR
The cost of 2 cycles, one motorcycle and one car is ₹ 289000, the cost of 3 cycles, 2 motorcycle and one car is ₹ 343500 and the cost of 1 cycle, 1 motorcycle and 2 cars is ₹ 514500. Represent the following information as linear equation. Solve them using matrix.
Question 25.
A diet for a sick person must contain atleast 4000 units of vitamins, 50 units of minerals and 1400 units of calories. Two foods A and B are available at a cost of ₹ 5 and ₹ 4 per unit respectively. One unit of the food A contains 200 units of vitamins, 1 unit of minerals and 40 units of calories while one unit of food B contains 100 units of vitamin, 2 units of minerals and 40 units of calories. Find what combination of the food A and B should be used to have least cost but it must satisfy the requirement of the sick person. Form LPP and solve graphically.
Question 26.
Two signboards, one circular and one square are to be made using a wire of length 40 m and cutting it into two pieces. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?
Question 27.
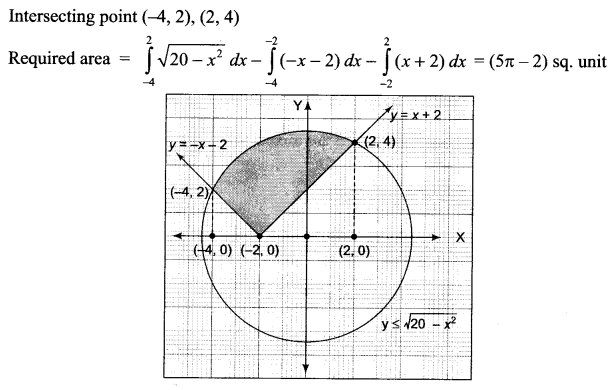
Using integration find the area of the region {(x, y): |x + 2| ≤ y ≤ √(20 – x2)}
OR
Draw a rough sketch of the curve y = cos2x in [0, π] and find the area enclosed by the curve, the line x = 0, x = π and y = 0.
Question 28.
Find the equation of a curve, if the slope of the tangent to the curve at any point (x, y) on it is given by \(\frac { y }{ x } -cos\left( \frac { y }{ x } \right) cot\left( \frac { y }{ x } \right)\) , (x > 0, y > 0) and the curve passes through the point (1, \(\frac { \pi }{ 4 }\))
Question 29.
Write the nature of the lines
![]()
Also find the shortest distance between them.
OR
Find the coordinates of the image of the point (1, 3, 4) in the plane 2x – y + z + 3 = 0
Solutions
Solution 1.
x = ±4
Solution 2.
Solution 3.
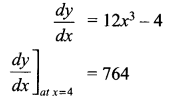
Solution 4.
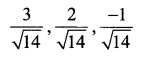
Solution 5.
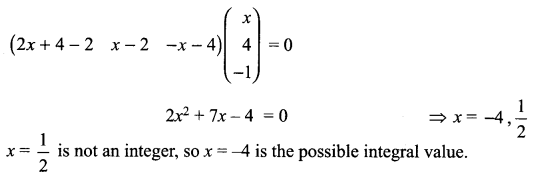
Solution 6.
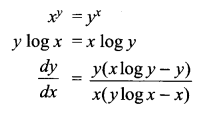
Solution 7.
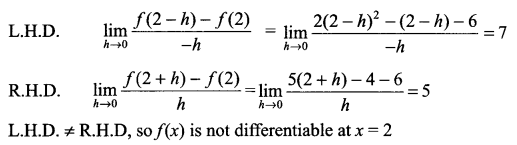
Solution 8.
Let radius of base of water level in conical funnel is r, at time t, its height is A and volume is V.
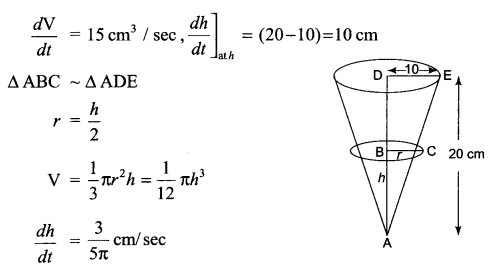
Solution 9.
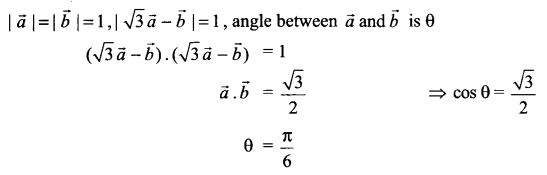
Solution 10.
S = {MFS, MSF, SFM, SMF, FMS, FSM}
E = {MFS, SFM, SMF, FMS}
F = {MFS, SFM} and
E ∩ F = {MFS, SFM}
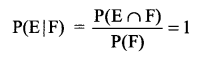
Solution 11.
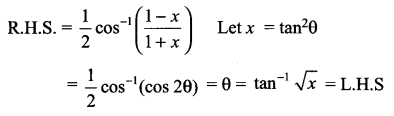
Solution 12.
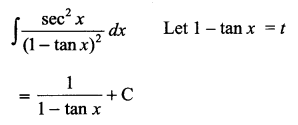
Solution 13.
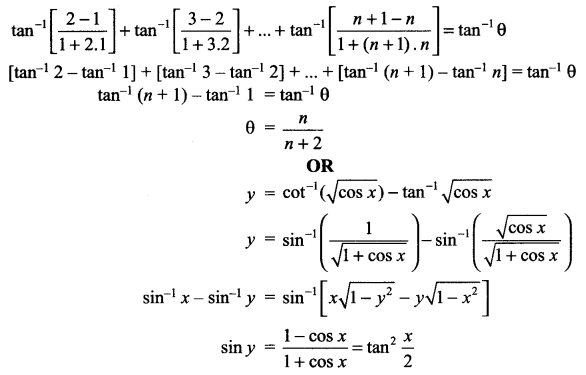
Solution 14.
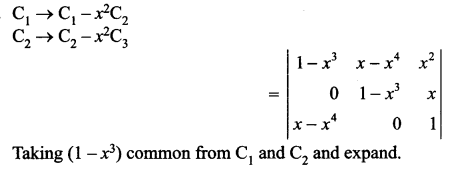
Solution 15.
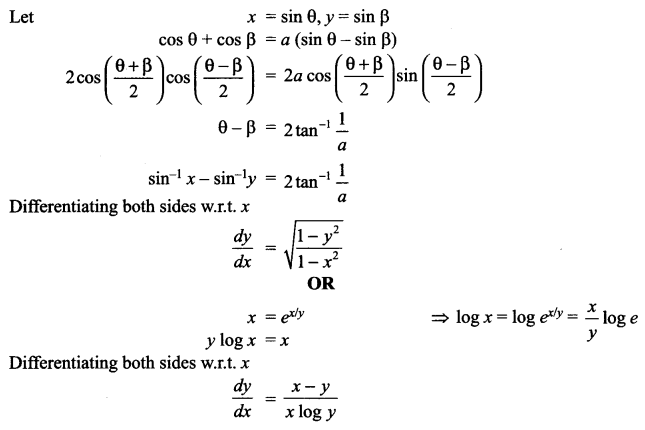
Solution 16.
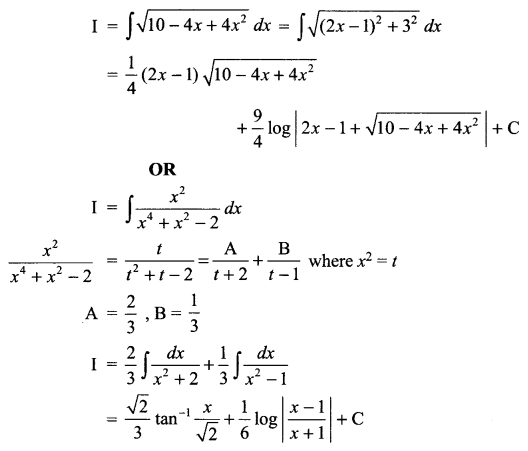
Solution 17.
Let a sin x + b cos x = A (cos x – sin x) + B (cos x + sin x)
Comparing both sides
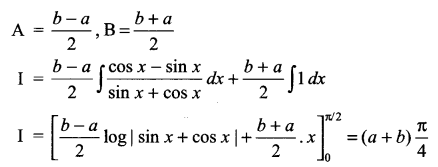
Solution 18.
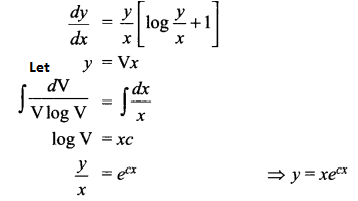
Solution 19.
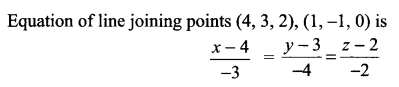

Solution 20.
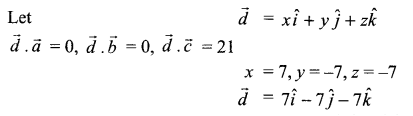
Solution 21.

Solution 22.
E1: Pan masala taken by man
E2: Pan masala taken by woman
A: X brand
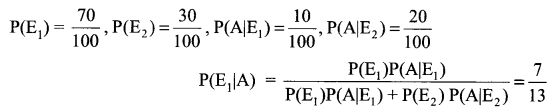
It causes several diseases including cancer.
Solution 23.
Prove it is reflexive, Prove it is symmetric, Prove it is transitive.
Because it is reflexive, symmetric and transitive, so R is an equivalence relation on N x N.
Solution 24.
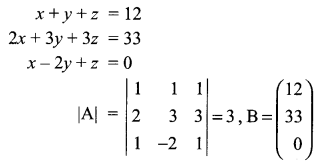
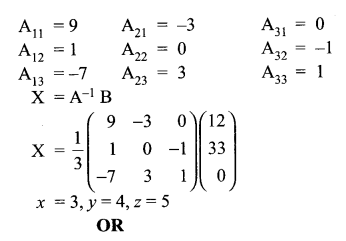
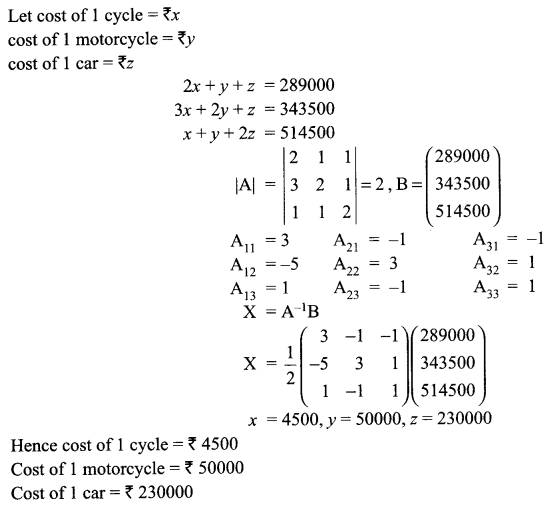
Solution 25.
Let x unit of food A and y unit of food B are mixed.
Objective function is minimise cost Z = 5x + 4y
Subject to constraints are
200x + 100y ≥ 4000 ⇒ x + 2y ≥ 50
40x + 40y ≥ 1400 ⇒ x, y ≥ 0
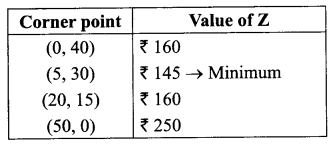
Here solution set is unbounded. So minimum value ₹ 145 may or may not be occur.
Take 5x + 4y < 145
Plot this by dotted line. Open half plane determined by 5x + 4y < 145 do not have a point common, so ₹ 145 is the minimum value when 5 units of food A and 30 units of food B are mixed.
Solution 26.

Solution 27.
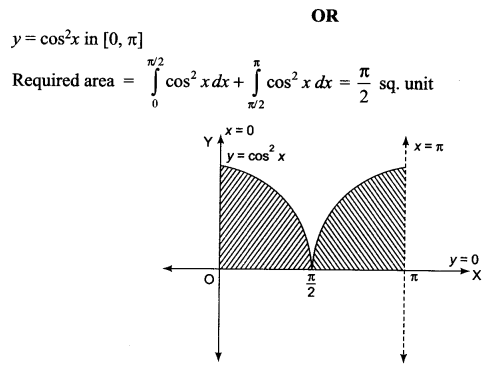
Solution 28.
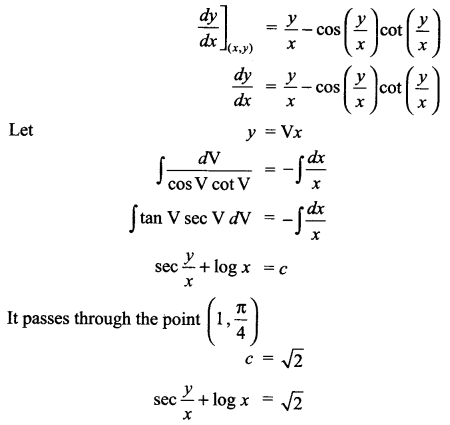
Solution 29.
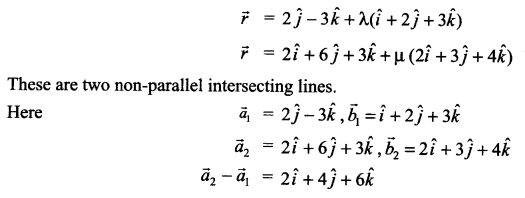
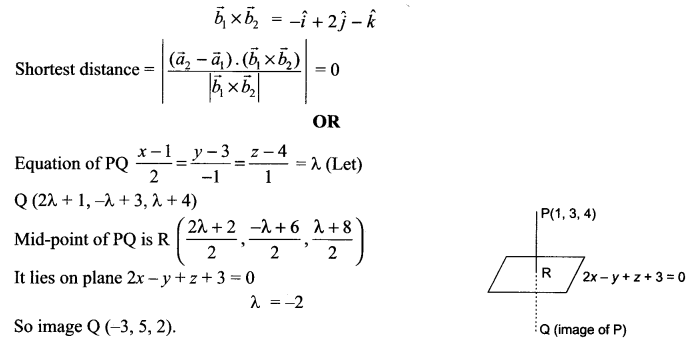
We hope the CBSE Sample Papers for Class 12 Maths Paper 7 help you. If you have any query regarding CBSE Sample Papers for Class 12 Maths Paper 7, drop a comment below and we will get back to you at the earliest.
