CBSE Sample Papers for Class 12 Maths Paper 6 are part of CBSE Sample Papers for Class 12 Maths. Here we have given CBSE Sample Papers for Class 12 Maths Paper 6.
CBSE Sample Papers for Class 12 Maths Paper 6
| Board | CBSE |
| Class | XII |
| Subject | Maths |
| Sample Paper Set | Paper 6 |
| Category | CBSE Sample Papers |
Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 6 of Solved CBSE Sample Paper for Class 12 Maths is given below with free PDF download solutions.
Time: 3 Hours
Maximum Marks: 100
General Instructions:
- All questions are compulsory.
- Questions 1-4 in section A are very short answer type questions carrying 1 mark each.
- Questions 5-12 in section B are short answer type questions carrying 2 marks each.
- Questions 13-23 in section C are long answer I type questions carrying 4 marks each.
- Questions 24-29 in section D are long answer II type questions carrying 6 marks each.
SECTION A
Question 1.
If A and B are square matrices of order 3 such that |A| = -1 and |B| = 3 then find the value of |7AB|.
Question 2.
Evaluate \(\int { \left( \sqrt { x } -\frac { 1 }{ \sqrt { x } } \right) } ^{ 2 }dx\)
Question 3.
Find the slope of the tangent to the curve y = x3 – 3x + 2 at the point whose x-coordinate is 3.
Question 4.
The equation of a line is given by \(\frac { x-4 }{ 2 } =\frac { y+3 }{ 3 } =\frac { z+2 }{ 6 }\). Write the direction cosines of a line parallel to the above line.
SECTION B
Question 5.
Give an example of two non-zero 2 x 2 matrices A and B such that AB = 0.
Question 6.
Find \(\frac { dy }{ dx }\) if x = a (θ – sin θ) and y = a (1 + cos θ).
Question 7.
Find the points on the curve x2 + y2 – 2x – 3 = 0 at which the tangents are parallel to x-axis.
Question 8.
Prove that the curves y2 = 4ax and xy = c2 cut at right angles if c4 = 32a4.
Question 9.
The two vectors \(\hat { j } +\hat { k }\) and \(3\hat { i } -\hat { j } +4\hat { k }\) represents the two sides AB and AC respectively of a ∆ABC. Find the length of the median through A.
Question 10.
Given that the events A and B are such that P(A) = \(\frac { 1 }{ 2 }\), P(B) = p, P(A ∪ B) = \(\frac { 3 }{ 5 }\), find p if they are independent.
Question 11.
Find the value of tan-1 √3 – cot-1 (-√3)
Question 12.
Evaluate \(\int { \frac { dx }{ x-\surd x } }\)
SECTION C
Question 13.
Find the greatest and the least value of (sin-1 x)2 + (cos-1 x)2.
Question 14.
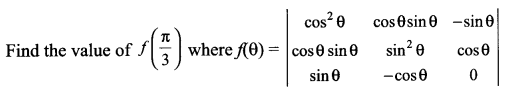
Question 15.
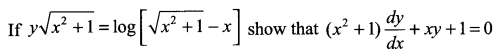
Question 16.
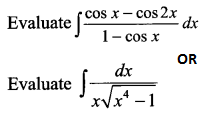
Question 17.
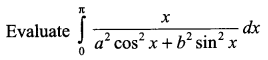
Question 18.
Find the general solution of the differential equation
\(\frac { dy }{ dx }\) = (3x + y + 1)2 dx
Question 19.
Find the equation of the plane passing through the points (2, 1, -1) and (-1, 3, 4) and perpendicular to the plane x – 2y + 4z = 10.
Question 20.
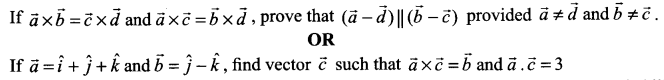
Question 21.
A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability distribution of the number of successes and hence find its mean.
Question 22.
There is a group of 100 people who are patriotic out of which 70 believe in non-violence. Two persons are selected at random out of them. Write the probability distribution for the selected persons who are non-violent. Also find the mean of the distribution. Explain the importance of non-violence in patriotism.
OR
A box of oranges is inspected by examining three randomly selected oranges drawn without replacement. If all the three oranges are good, the box is approved for sale otherwise it is rejected. Find the probability that the box containing 15 oranges out of which 12 are good and 3 are bad ones will be approved for sale. Which values are reflected when boxes are approved for sale?
Question 23.
If A and B are two non-empty sets, show that the function f : A x B → B x A defined by f(a, b) = (b, a) is bijective.
SECTION D
Question 24.
Using matrices, solve the following system of equations:
8x + 4y + 3z = 18
2x + y + z = 5
x + 2y + z = 5
Question 25.
An aeroplane can carry a maximum of 200 passengers. A profit of ₹ 1000 is made on each first class ticket and a profit of ₹ 600 is made on each economy class ticket. The airline reserves atleast 20 seats for first class. However atleast 4 times as many passengers prefer to travel by economy class as by first class. Determine how many tickets of each type must be sold in order to maximise the profit of the airline. What is the maximum profit? Formulate the above LPP mathematically and solve it graphically.
Question 26.
Prove that the area of a right angle triangle inscribed in a circle, is maximum when the triangle is isosceles.
OR
A square tank of capacity 250 cubic metres has to be dugout. The cost of the land is ₹ 50 per square metre. The cost of digging increases with the depth and for the whole tank it is ₹ 400 x h2 where h metres is the depth of the tank. What should be the dimensions of the tank so that the cost be minimum?
Question 27.
Find the area of the region in the first quadrant enclosed by x-axis, line x = √3 y and the circle x2 + y2 = 4.
OR
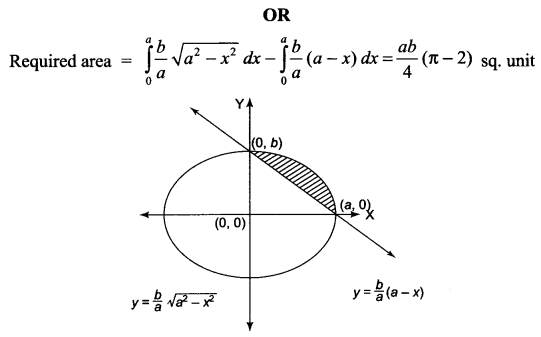
Find the area of the smaller region bounded by the ellipse \(\frac { { x }^{ 2 } }{ { a }^{ 2 } } +\frac { { y }^{ 2 } }{ { b }^{ 2 } } =1\) and the straight line \(\frac { { x } }{ { a } } +\frac { { y } }{ { b } } =1\)
Question 28.
Find the particular solution of the differential equation satisfying the given condition x2dy + (xy + y2)dx = 0; y = 1 when x = 1
Question 29.
Find the equation of the plane passing through the line of intersection of the planes x – 2y + z = 1 and 2x + y + z = 8 and parallel to the line with direction ratios 1, 2, 1. Also find the perpendicular distance of the point P(3, 1, 2) from this plane.
OR
Find the distance of the point (2, 3, 4) from the plane 3x + 2y + 2z + 5 = 0 measured parallel to the line \(\frac { x+3 }{ 3 } =\frac { y-2 }{ 6 } =\frac { z }{ 2 }\)
Solutions
Solution 1.
|A| = -1, |B| = 3
|7AB| = 73 |A| |B| = -1029
Solution 2.
\(\frac { { x }^{ 2 } }{ 2 }\) + log x – 2x + C
Solution 3.
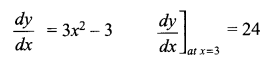
Solution 4.
Direction ratios of a line parallel to given line -2, 3, 6 and direction cosines will be \(\frac { -2 }{ 7 }\) , \(\frac { 3 }{ 7 }\) , \(\frac { 6 }{ 7 }\)
Solution 5.
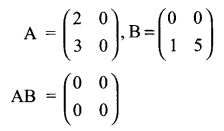
Solution 6.
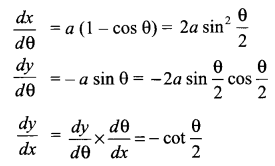
Solution 7.
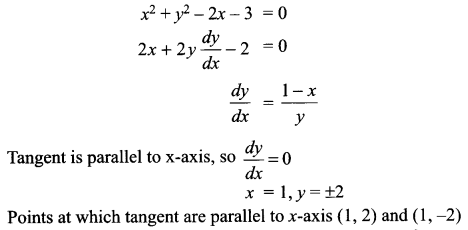
Solution 8.

Solution 9.
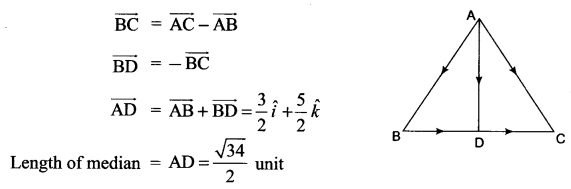
Solution 10.
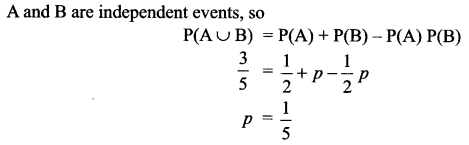
Solution 11.
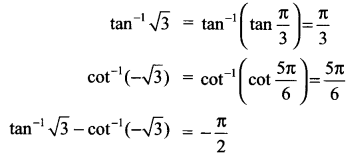
Solution 12.
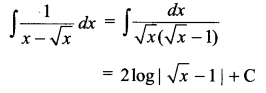
Solution 13.
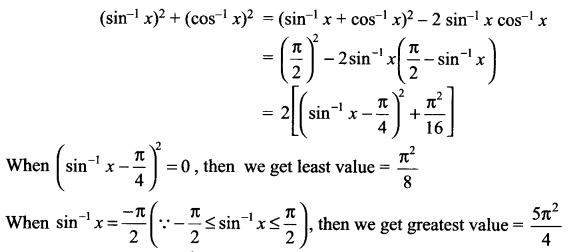
Solution 14.
Taking cos2 θ common from R1, cosθ sinθ from R2 and sinθ from R3, then R2 → R1, R3 → R3 – R1 and expand
f(θ) = 1
f(\(\frac { \pi }{ 3 }\)) = 1
Solution 15.
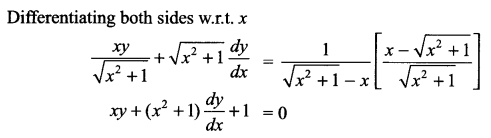
Solution 16.
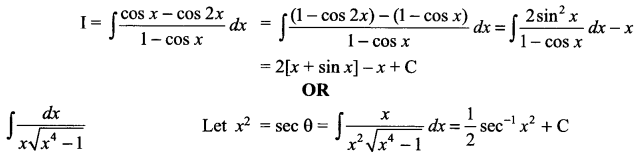
Solution 17.
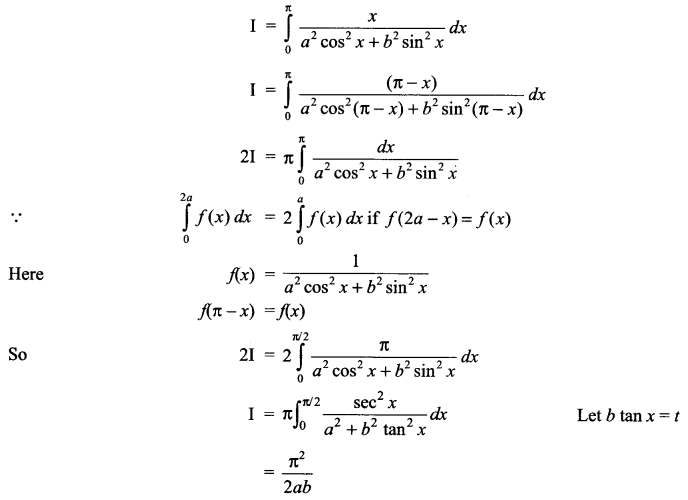
Solution 18.
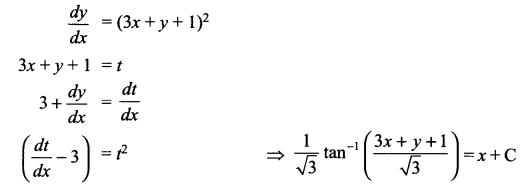
Solution 19.
Plane equation passing through point (2, 1, -1) is
a(x – 2) + b(y – 1) + c(z + 1) = 0 ……..(1)
Point (-1, 3, 4) passes through (1), -3a + 2b + 5c = 0 ……(2)
Plane (1) ⊥ to x – 2y + 4z = 10, so a – 2b + 4c = 0 …….(3)
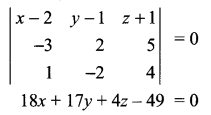
Solution 20.

Solution 21.

Solution 22.
Total number of people in group = 100
Number of people believe in non-violence = 70
Number of people believe in violence = 30
Two persons are selected at random without replacement X : 0, 1, 2

Non-violence helps in presenting your views in a peaceful manner.
OR
Total oranges = 15, good oranges = 12, bad oranges = 3
3 oranges are selected at random without replacement. Box is approved for sale if all the three selected oranges are good.

Value reflected is honesty.
Solution 23.
First prove one-one. Prove onto.
Because it is one-one and onto, so it is bijective.
Solution 24.
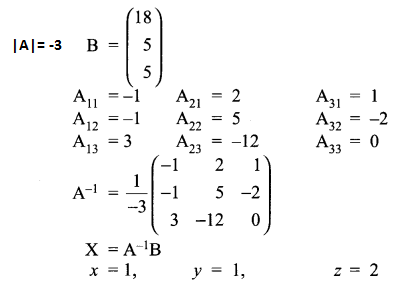
Solution 25.
Number of first class tickets = x
Number of economy class tickets = y
Objective function is maximise profit Z = 1000 x + 600 y
Subject to constraints are
x + y ≤ 200
x ≥ 20
y ≥ 4x
x, y ≥ 0
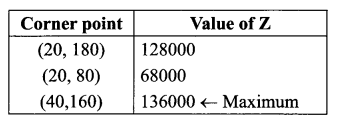
Hence maximum profit is ₹ 136000 when 40 first class tickets and 160 economy class tickets are sold.
Solution 26.

Solution 27.
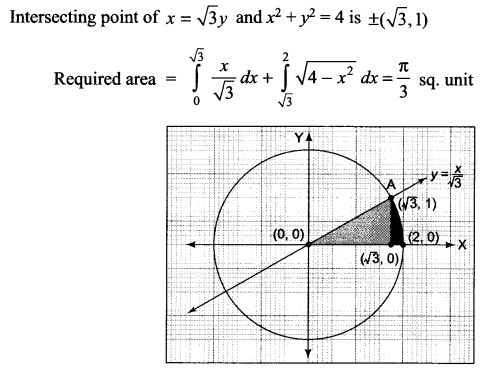
Solution 28.
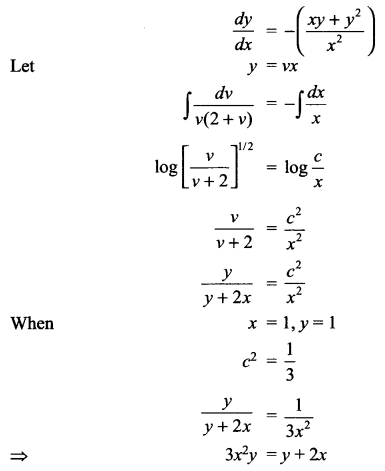
Solution 29.


We hope the CBSE Sample Papers for Class 12 Maths Paper 6 help you. If you have any query regarding CBSE Sample Papers for Class 12 Maths Paper 6, drop a comment below and we will get back to you at the earliest.
