CBSE Sample Papers for Class 12 Maths Paper 4 are part of CBSE Sample Papers for Class 12 Maths. Here we have given CBSE Sample Papers for Class 12 Maths Paper 4.
CBSE Sample Papers for Class 12 Maths Paper 4
| Board | CBSE |
| Class | XII |
| Subject | Maths |
| Sample Paper Set | Paper 4 |
| Category | CBSE Sample Papers |
Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 4 of Solved CBSE Sample Paper for Class 12 Maths is given below with free PDF download solutions.
Time: 3 Hours
Maximum Marks: 100
General Instructions:
- All questions are compulsory.
- Questions 1-4 in section A are very short answer type questions carrying 1 mark each.
- Questions 5-12 in section B are short answer type questions carrying 2 marks each.
- Questions 13-23 in section C are long answer I type questions carrying 4 marks each.
- Questions 24-29 in section D are long answer II type questions carrying 6 marks each.
SECTION A
Question 1.
If A is a skew symmetric matrix of order 3 x 3 then prove that |A| = 0
Question 2.
Check the continuity of the function
Question 3.
Find the anti derivative of sin 2x by the method of inspection
Question 4.
If the line is parallel to the plane 3x – 2y + cz = 14 then find the value of c.
SECTION B
Question 5.
Determine the value of x for which the matrix
Question 6.
Question 7.
Verify Mean Value Theorem for f(x) = (x – 1) (x – 2) (x – 3) in [1, 4]
Question 8.
Find the approximate value of f(3.01) when f(x) = 3x2 + 5x + 4.
Question 9.
Find the angle between the pair of lines
Question 10.
Evaluate P(A ∪ B) if 2P(A) = P(B) = and P(A|B) =
Question 11.
Reshma wishes to mix two types of food P and Q in such a way that the vitamin contents of the mixture contain atleast 8 units of vitamin A and 11 units of vitamin B. Food P costs ₹ 60/kg and food Q costs ₹ 80/kg. Food P contains 3 units/ kg of vitamin A and 5 units/kg of vitamin B while food Q contains 4 units/kg of vitamin A and 2 units/kg of vitamin B. Formulate the L.P.P for minimum cost of the mixture.
Question 12.
Evaluate
SECTION C
Question 13.
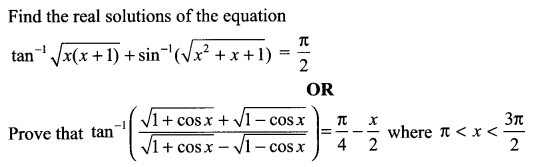
Question 14.

Question 15.
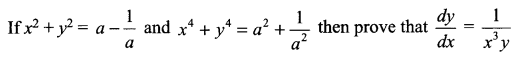
Question 16.
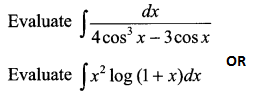
Question 17.
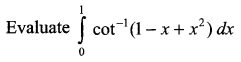
Question 18.
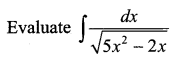
Question 19.
![]()
Question 20.
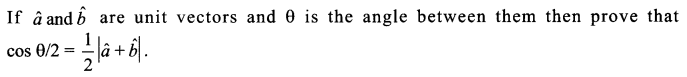
Question 21.
40% students of a college reside in hostel and the remaining reside outside. At the end of the year, 50% of the hostellers got A grade while from outside students, only 30% got A grade in the examination. At the end of year, a student of the college was choosen at random and was found to get A grade. What is the probability that the selected student was a hosteller ?
Question 22.
Three distinguishable balls are distributed in three cells. Find the conditional probability that all the three occupy the same cell given that atleast two of them are in the same cell. Which values are reflected from tricolour of our national flag?
Question 23.
Solve the following L.P.P. graphically.
Maximise Z = 8000 x + 12000 y
Subject to constraints are
9x + 12y ≤ 180
x + 3y ≤ 30
x, y ≥ 0
SECTION D
Question 24.
Let A = {1, 2, 3, … 9} and R be the relation in A x A defined by (a, b) R (c, d). If a + d = b + c for a, b, c, d ∈ A, prove that R is an equivalence relation. Also obtain the equivalence class (2, 5).
OR
Let A = R – {3} and B = R – {1}. Let f : A → B defined by f(x) = for all x ∈ A. Then show that f is bijective. Hence find f-1(x). Also find the value of f-1(17).
Question 25.
Find the area of the region bounded by the curves y = tan x, the tangent drawn to the curve y = tan x at x = and the x-axis using integration.
OR
Find the area enclosed by the curves y = |x – 1| and y = 1 – |x – 1| using integration.
Question 26.
Show that the four points (0, -1, -1), (-4, 4, 4), (4, 5, 1) and (3, 9, 4) are coplanar. Find the equation of the plane containing them.
OR
Find the angle between the tangents to the parabolas y2 = 4ax and x2 = 4by at their point of intersection other than the origin.
Question 27.

Question 28.
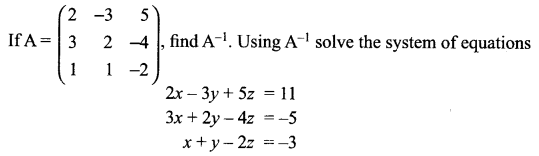
Question 29.
A plot is in the form of a rectangle with a semicircular plot along one of the shorter sides. The perimeter of the total plot is 100 m. A farmer wants to use the maximum area for growing the grass. Find the dimensions of the plot so that maximum grass can be planted.
Solutions
Solution 1.
A is a skew symmetric matrix, so A’ = -A
|A’| =|-A| ⇒ |A| = -|A|
|A| =0
Solution 2.
At x = 1,
L.H.L = 1
R.H.L = 5
L.H.L ≠ R.H.L, so f(x) is discontinuous at x = 1
Solution 3.
cos 2x
Solution 4.
2(3) + 1 (-2) + 2c = 0
⇒ c = -2
Solution 5.
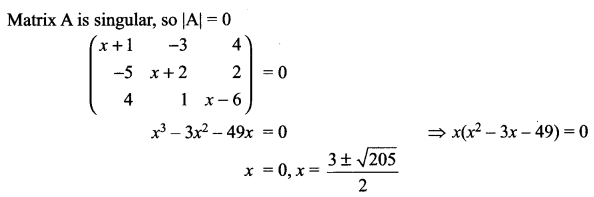
Solution 6.
Solution 7.
f(x) is continuous in [1, 4]
f(x) is differentiable in ]1, 4[
Solution 8.
x + ∆x = 3.01, x = 3
∆x = 0.01
f(x + ∆x) =f(x) + f'(x) ∆x
f(3.01) =f(3) + f'(3) (0.01) = 46 + 23 (0.01) = 46.23
Solution 9.
Solution 10.
Solution 11.
Let food P consist x kg and food Q consist y kg in mixture.
Objective function is minimise cost Z = 60x + 80y
Subject to constraints are
3x + 4y ≥ 8
5x + 2y ≥ 11
x, y ≥ 0
Solution 12.
Solution 13.
Solution 14.
Taking a, b, c common from C1, C2, C3
after that R1 → R1 – R2 – R3
after this C1 → C1 – C2 and expand
OR
R1 → R1 – R2, R2 → R2 – R3
Taking (x – y),(y – z) common from R1 and R2
Then R1 → R1 – R2, R3 → R3 – zR2
Then taking (x – z) common from R1 and expand.
Solution 15.
Solution 16.
Solution 17.
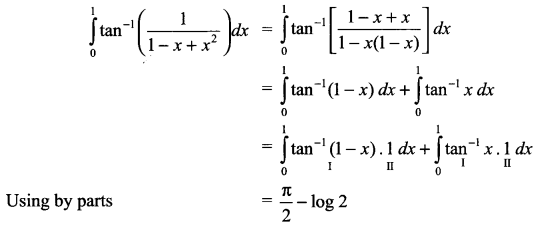
Solution 18.
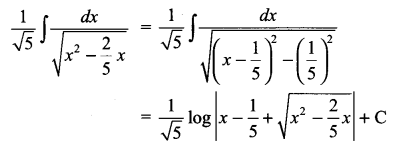
Solution 19.
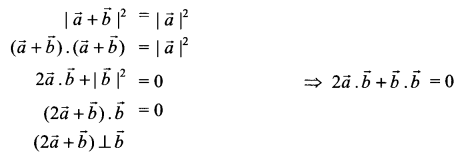
Solution 20.
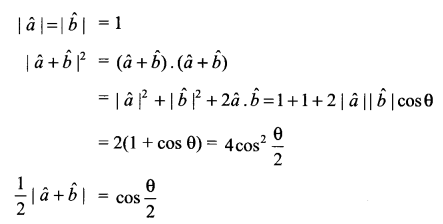
Solution 21.
E1: student of a college reside in Hostel
E2: student of a college reside outside
A: student got A grade
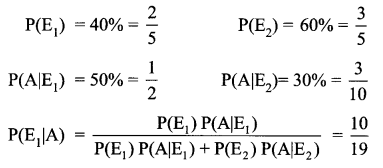
Solution 22.
E1: All the three balls are in the same cell.
E2: At least two balls are in the same cell.
Since each ball can be place in a cell in 3 ways, so three distinct balls can be place in three cells by 3 x 3 x 3 = 27 ways.
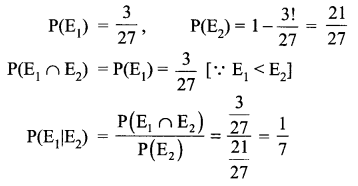
In tricolour:
Orange – strength and courage
White – peace and truth
Green – growth and fertility
Solution 23.
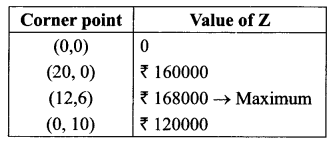
Solution 24.
Prove reflexive, Prove symmetric, Prove transitive
R is reflexive, symmetric and transitive, so R is an equivalence relation.
Equivalence class (2, 5) is (p, q) ⇒ 2 + q = 5 + p
So (1, 4), (2, 5), (3, 6), (4, 7), (5, 8), (6, 9)
OR
Prove one-one, Prove onto
f is one-one and onto, so it is bijective
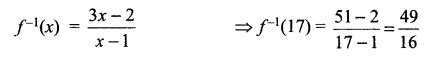
Solution 25.
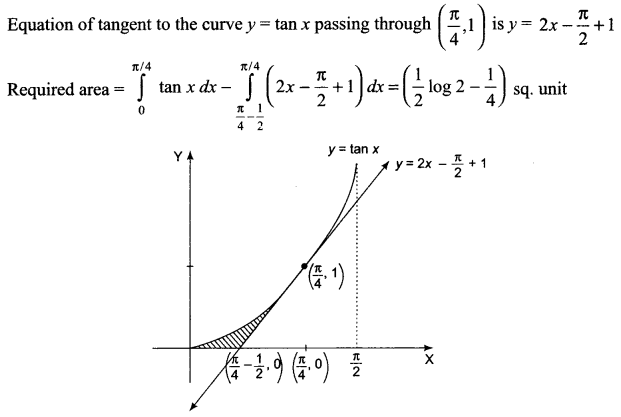
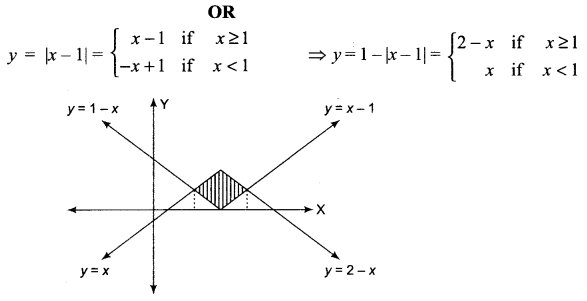
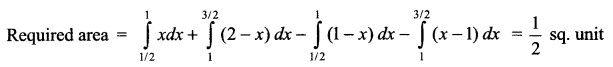
Solution 26.
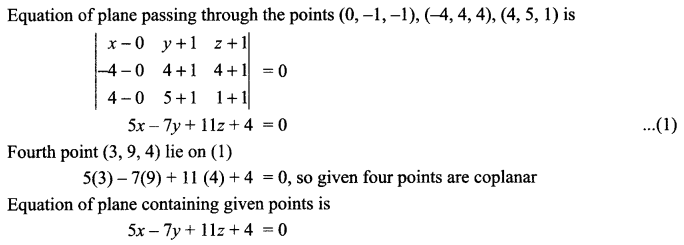

Solution 27.
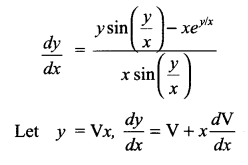
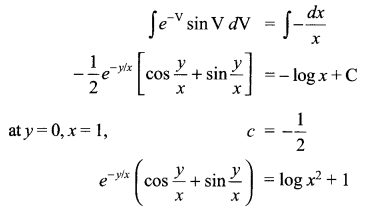
Solution 28.
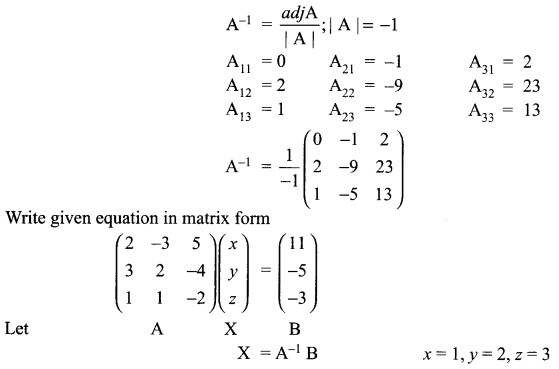
Solution 29.
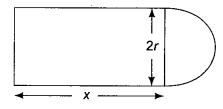
Let length of rectangular plot = x m
breadth of rectangular plot = 2r m
radius of semicircle = r m
x + x + 2r + πr = 100


We hope the CBSE Sample Papers for Class 12 Maths Paper 4 help you. If you have any query regarding CBSE Sample Papers for Class 12 Maths Paper 4, drop a comment below and we will get back to you at the earliest.
