CBSE Sample Papers for Class 12 Maths Paper 2 are part of CBSE Sample Papers for Class 12 Maths. Here we have given CBSE Sample Papers for Class 12 Maths Paper 2.
CBSE Sample Papers for Class 12 Maths Paper 2
| Board | CBSE |
| Class | XII |
| Subject | Maths |
| Sample Paper Set | Paper 2 |
| Category | CBSE Sample Papers |
Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 2 of Solved CBSE Sample Paper for Class 12 Maths is given below with free PDF download solutions.
Time: 3 Hours
Maximum Marks: 100
General Instructions:
- All questions are compulsory.
- Questions 1-4 in section A are very short answer type questions carrying 1 mark each.
- Questions 5-12 in section B are short answer type questions carrying 2 marks each.
- Questions 13-23 in section C are long answer I type questions carrying 4 marks each.
- Questions 24-29 in section D are long answer II type questions carrying 6 marks each.
SECTION A
Question 1.
What is the distance between the planes 2x + 2y – z + 2 = 0 and 4x + 4y – 2z + 5 = 0?
Question 2.
Evaluate ∫1−2|x|xdx∫1−2|x|xdx
Question 3.
If A=(2175) , find |A (adj A)|.
Question 4.
If f(x) = ∫x0tsintdt then find the value of f'(x).
SECTION B
Question 5.
If A and B are two events such that P(A) = 14, P(B) = 12 and P(A ∩ B) = 18, find P (not A and not B).
Question 6.
A manufacturer produces two types of suitcase. He has two machines A and B. The first type of suitcase requires 3 hours on machine A and 3 hours on machine B. The second type of suitcase requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit ₹ 30 and ₹ 25 per suitcase of the first type and second type respectively. Formulate on L.P.P. for finding how many suitcase of each type must be make each day to make maximum profit?
Question 7.
Evaluate ∫dxx(x5+3)
Question 8.
Find the value of k so that the function
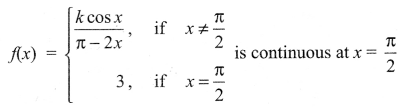
Question 9.
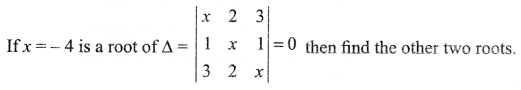
Question 10.
Find the condition that the curves 2x = y2 and 2xy = k intersect orthogonally.
Question 11.
Find the angle between the following pair of lines:
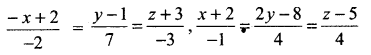
and check whether the lines are parallel or perpendicular.
Question 12.
Two dice are tossed. Find whether the following two events A and B are independent.
A = {(x, y) : x + y = 11}, B = {(x, y): x ≠ 5}, where (x, y) denote a typical sample point.
SECTION C
Question 13.
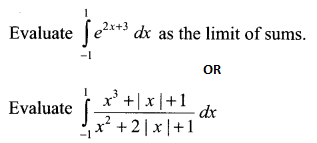
Question 14.

Question 15.
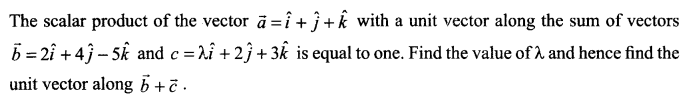
Question 16.
A problem in mathematics is given to three students whose chances of solving it are 12, 13 , 14 respectively. What is the probability that only one of them solves it correctly? Which ideal condition will you keep in your mind while solving the problem?
Question 17.
Solve the following equations for x
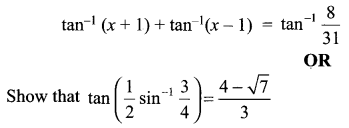
Question 18.

Question 19.
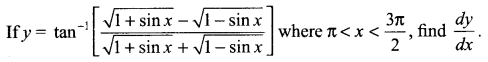
Question 20.
A letter is known to have come from TATA NAGAR or CALCUTTA. On the envelope, just two consecutive letters TA are visible. What is the probability that letter has come from (i) CALCUTTA (ii) TATA NAGAR.
Question 21.
Solve the following L.P.P graphically.
Maximize Z = 0.75x + 0.50y
Subject to constraints are
2x + y ≤ 60
x ≤ 20
2x + 3y ≤ 120
x, y ≥ 0
Question 22.
Evaluate ∫2π011+esinxdx
Question 23.
If ˉa, ˉb, ˉc are the position vectors of the vertices A, B, C of a ∆ABC respectively. Find an expression for the area of ∆ABC and hence deduce the condition for the points A, B, C to be collinear.
SECTION D
Question 24.
Find the area of the region included between the parabola y = 3x24 and the line 3x – 2y + 12 = 0.
OR
Find the area bounded by the curve y = √x, x = 2y + 3 in the first quadrant and x-axis.
Question 25.
Show that the general solution of the differential equation dydx+y2+y+1x2+x+1=0 is given by (x + y + 1) = A (1 – x – y – 2xy) where A is arbitrary constant.
Question 26.
Find the Cartesian as well as the vector equations of the planes through the intersection of the planes ˉr⋅(2ˆi+6ˆj)+12=0 and ˉr⋅(3ˆi−ˆj+4ˆk)=0 which are at a unit distance from the origin.
Question 27.
Two schools P and Q want to award their selected students on the values of discipline, politeness and punctuality. The school P wants to award ₹ x each, ₹ y each, ₹ z each for the three respective values to its 3, 2 and 1 students with a total award money of ₹ 1000. School Q wants to spend ₹ 1500 to award its 4, 1 and 3 students on the respective values (by giving the same award money for the three values as before). If the total amount of awards for one prize on each value is ₹ 600 using matrices, find the award money for each value.
Question 28.
A point on the hypotenuse of a right angled triangle is at distances a and b from the sides. Show that the minimum length of the hypotenuse is (a2/3 + b2/3)3/2.
OR
The sum of the surface areas of cuboids with sides x, 2x and x3 and a sphere is given to be constant. Prove that the sum of their volumes is minimum if x = 3 radius of sphere. Also find the minimum value of the sum of their volume.
Question 29.
Let R be the relation defined on set A = {1, 2, 3, 4, 5} by R = {(a, b) : |a – b| is even}. Show that R is an equivalence relation. Also show that all the elements of the subset {2, 4, 6} are related to each other and all the elements of the subset {1, 3, 5} are related to each other, but no element of the subset {2, 4} is related to an element of the subset {1, 3, 5}.
Solutions
Solution 1.
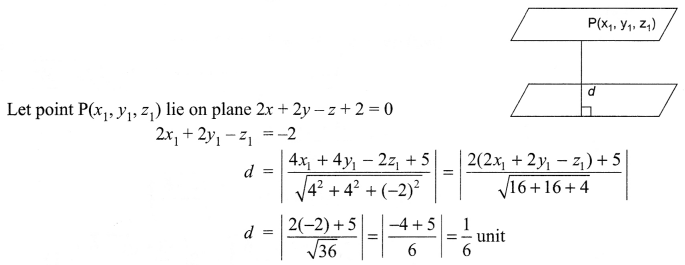
Solution 2.
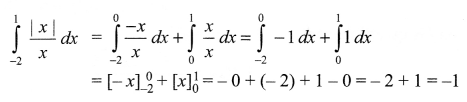
Solution 3.
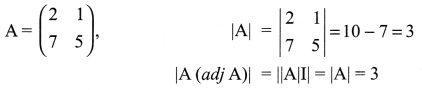
Solution 4.
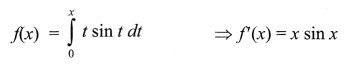
Solution 5.
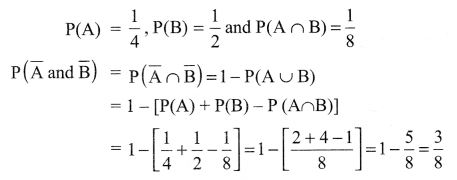
Solution 6.
Let x suitcase of type I
y suitcase of type II is manufactured
Objective function is maximize profit Z = 30x + 25y
Subject to constraints are
3x + 3y ≤ 18 (machine A constraint)
3x + 2y ≤ 15 (machine B constraint)
x, y ≥ 0 (non-negative constraint)
Solution 7.
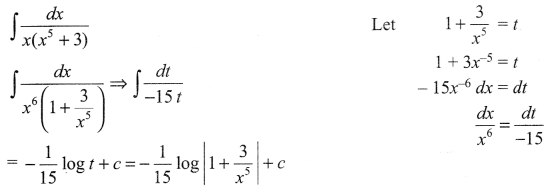
Solution 8.

Solution 9.
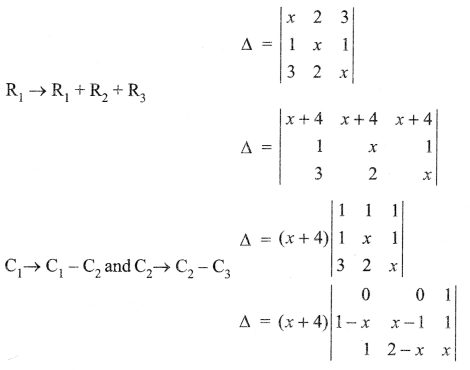
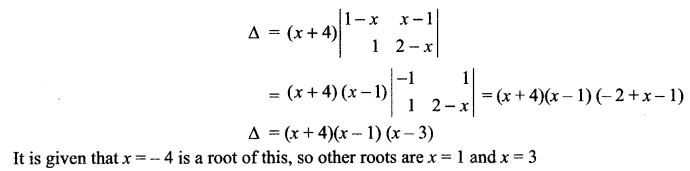
Solution 10.
2x = y2 ……. (1)
2xy = k ……(2)
Differentiating both sides w.r.t. x.
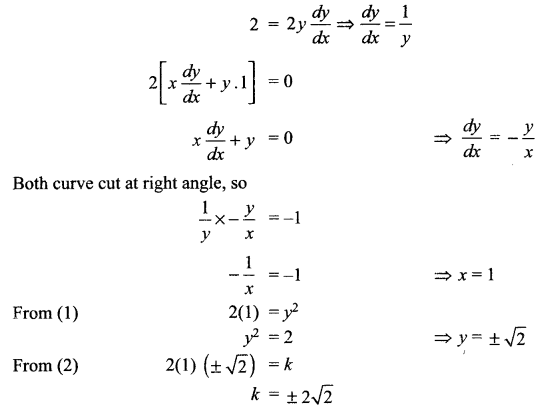
Solution 11.
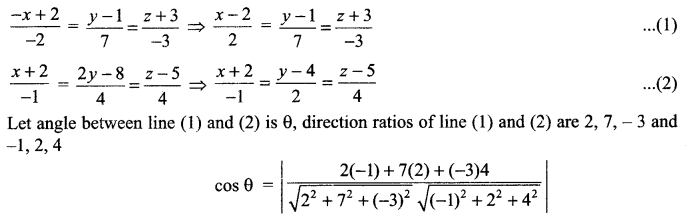
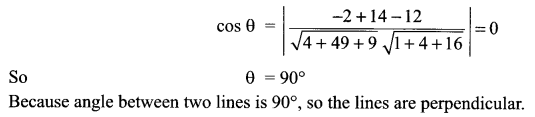
Solution 12.
Total possible outcomes = 36
A= {(x, y) : x + y = 11}, B = {(x, y) : x ≠ 5}
A = {(5, 6), (6, 5)}
B = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2) (2, 3), (2, 4) (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5) (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
A ∩ B = {(6, 5)}
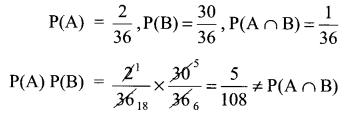
So A and B are not independent.
Solution 13.
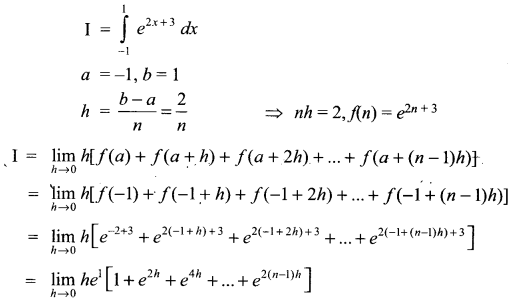
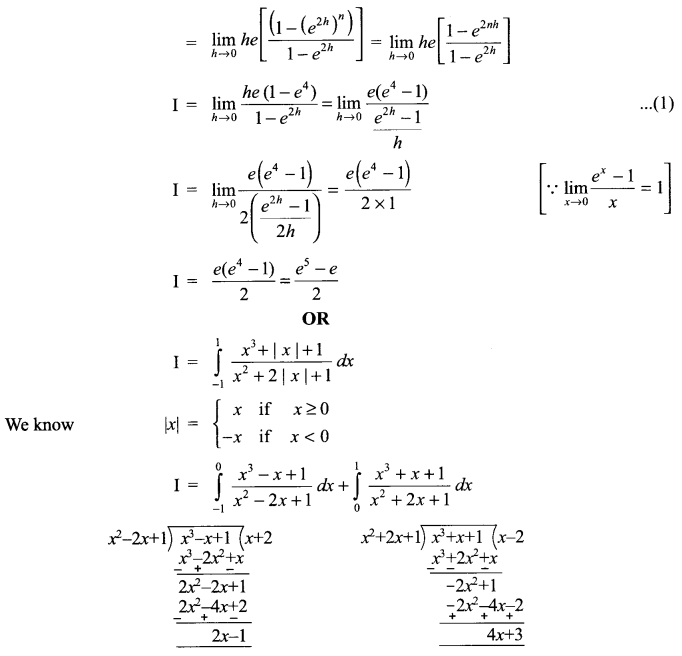
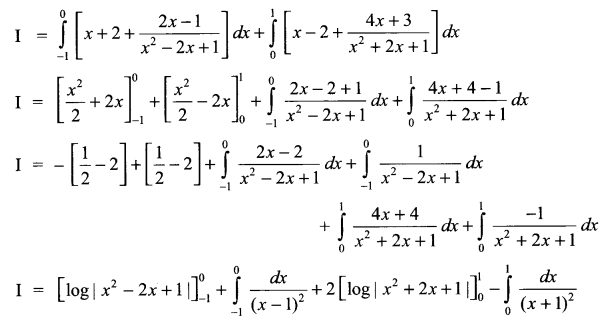
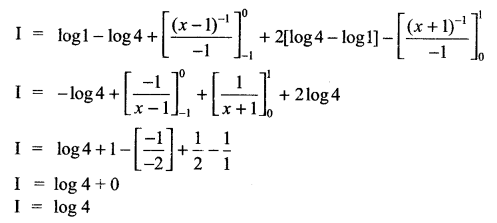
Solution 14.

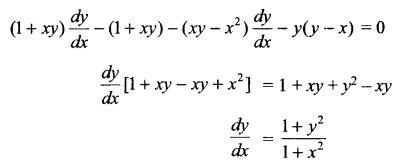
Solution 15.

Solution 16.
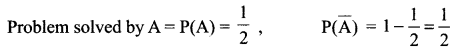

Solution 17.

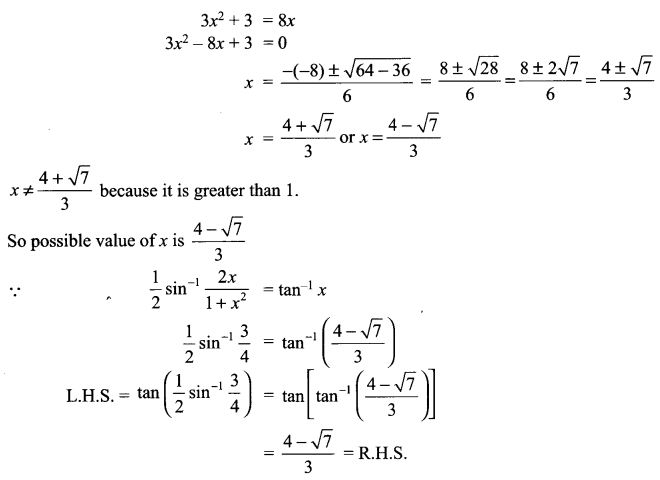
Solution 18.


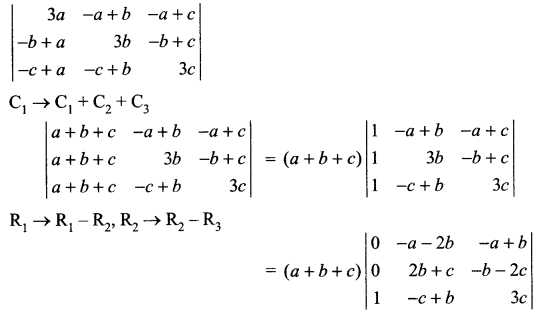
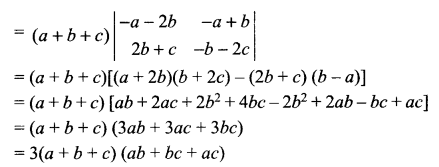
Solution 19.
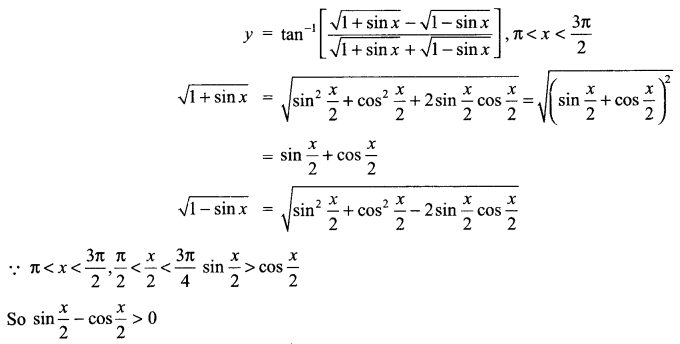
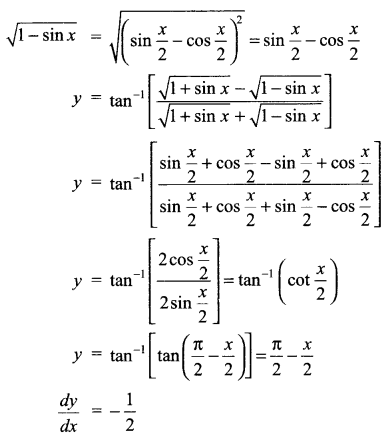
Solution 20.
Let E1 is the event: letter has come from TATA NAGAR
E2 is the event: letter has come from CALCUTTA
A is the event: two consecutive visible letters are TA
P(E1) = P(E2) = 12
In word TATA NAGAR total letters = 9
There are 8 groups of two consecutive letters TA, AT, TA, AN, NA, AG, GA, AR
Here ‘TA’ has come two times
P(A|E1) = 28 = 14
In word CALCUTTA total letters = 8.
So there are 7 groups of two consecutive letters CA, AL, LC, CU, UT, TT, TA
Here TA has come 1 time
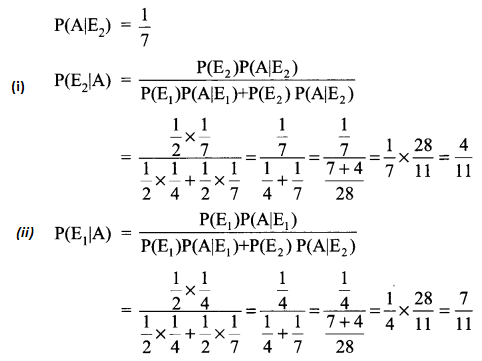
Solution 21.
Z = 0.75x + 0.50y
2x + y = 60
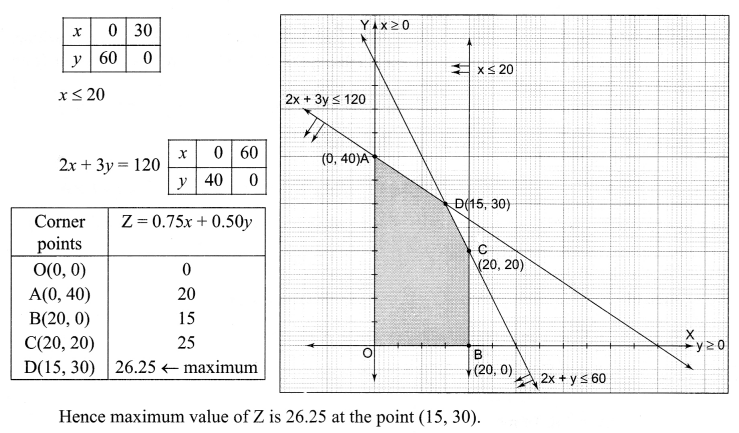
Solution 22.
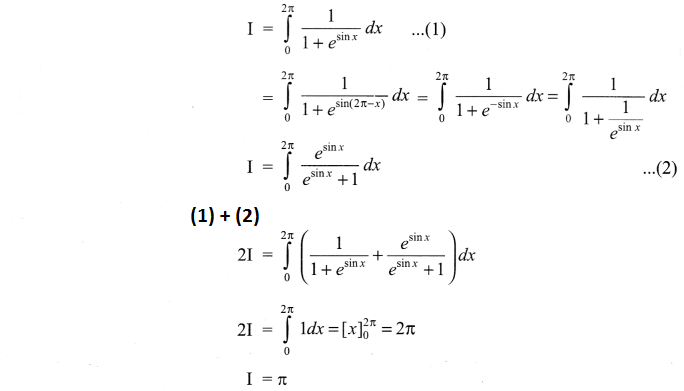
Solution 23.
Position vector of the vertices A, B, C are ˉa, ˉb, ˉc
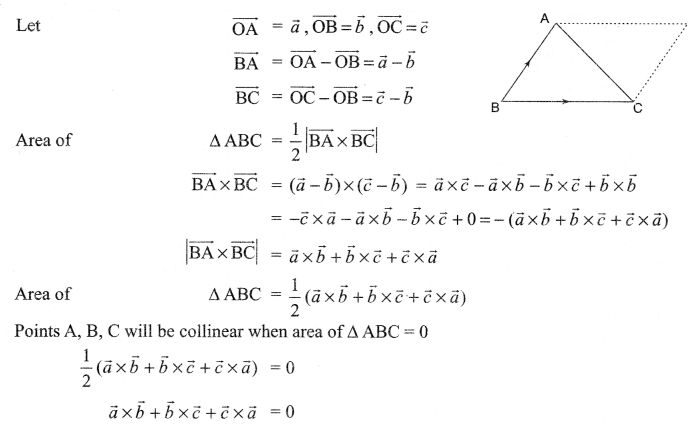
Solution 24.

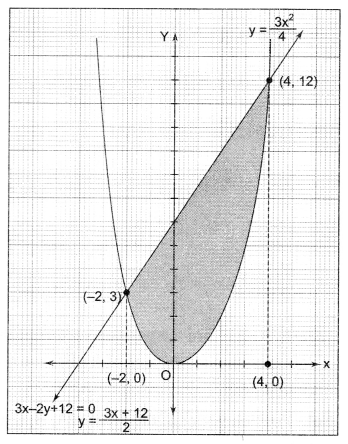

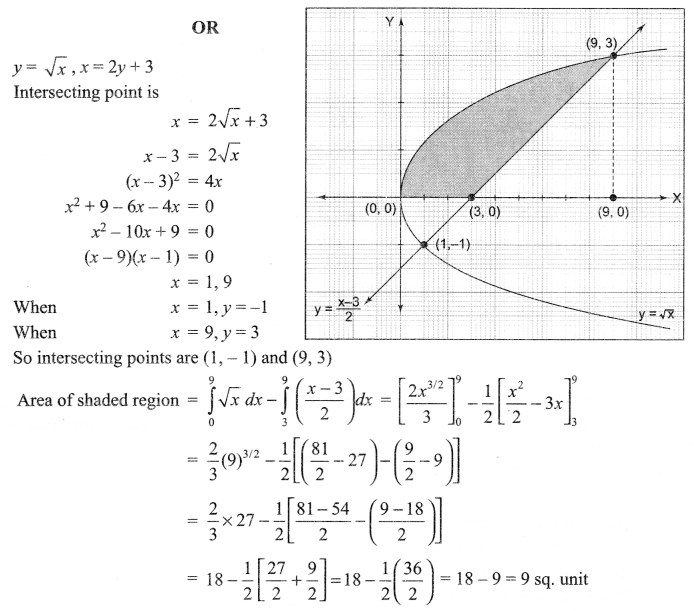
Solution 25.
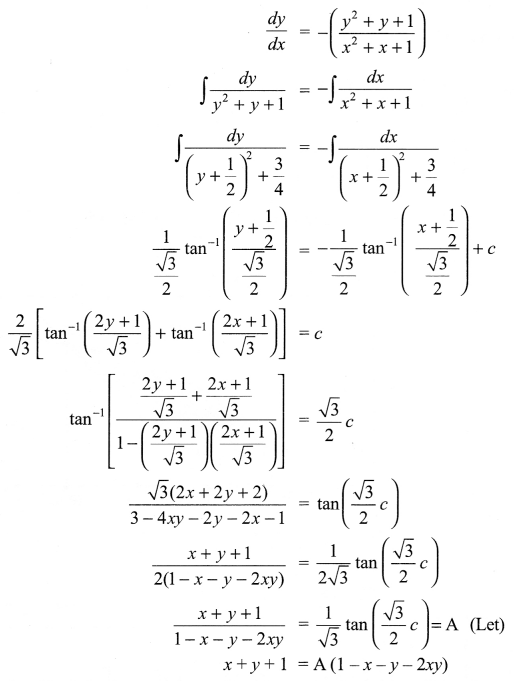
Solution 26.
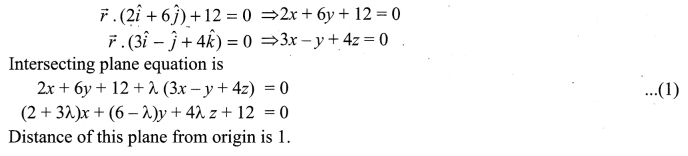
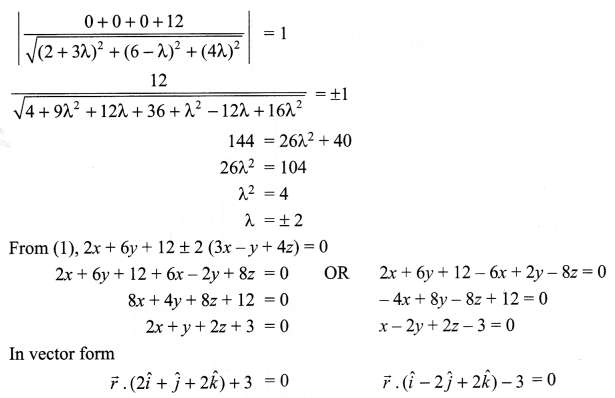
Solution 27.
3x + 2y + z = 1000
4x + y + 3z = 1500
x + y + z = 600
In matrix form
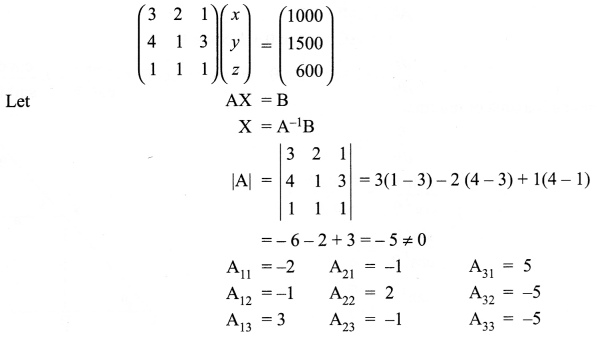
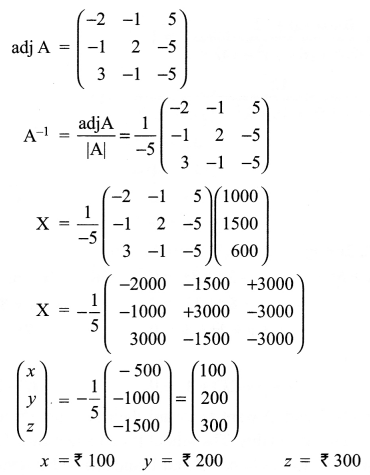
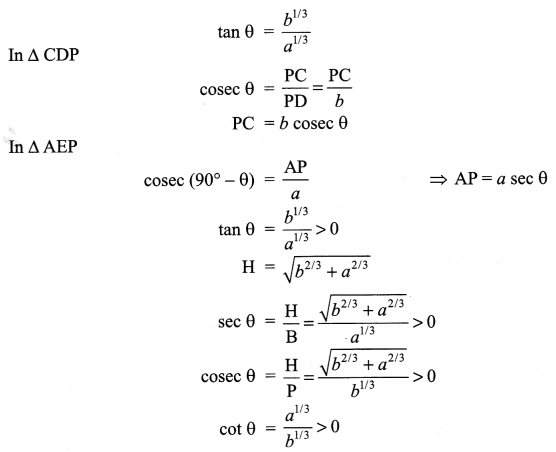
Solution 28.
Let P is any point on the hypotenuse AC
AC = AP + PC
z = AC = a sec θ + b cosec θ
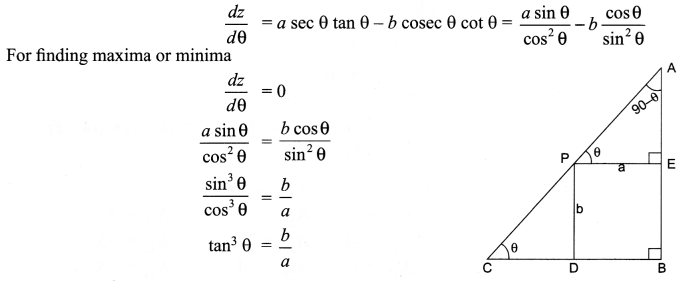


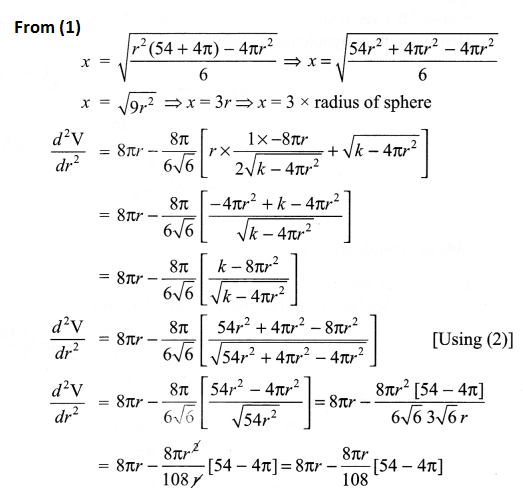
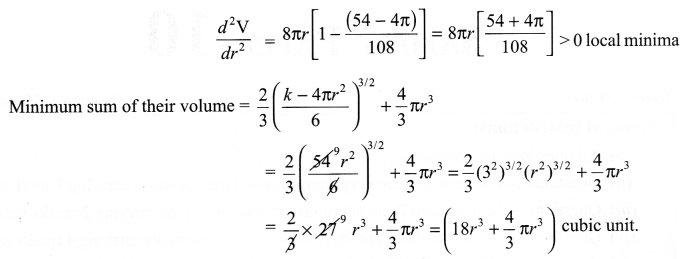
Solution 29.
A ={1, 2, 3, 4, 5}
R = {(a, b) : |a – b| is even}
R = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (1, 3), (3, 1), (1, 5), (5, 1), (2, 4), (4, 2), (3, 5), (5, 3)}
Reflexive: As |a – a| = 0 (an even number)
(a, a) ∈ R So R is reflexive.
Symmetric: (a, b) ∈ R
|a – b| is even = |-(b – a)| is even = |b – a| is even = (b, a) ∈ R
So R is symmetric.
Transitive: (a, b) ∈ R, (b, c) ∈ R
⇒ |a – b| is even and |b – c| is even
⇒ |a – b| is even and (b – c) is even = (a – b + b – c) is even = (a – c) is even = |a – c| is even = (a, c) ∈ R
So R is transitive.
R is reflexive, symmetric and transitive, so R is an equivalence relation.
as |1 – 3|, |3 – 1|, |3 – 5|, |5 – 3| and |1 – 5|, |5 – 1| are even numbers.
Therefore all elements of {1, 3, 5} are related to each other.
Also |2 – 4|, |4 – 2| is even. So all elements of {2, 4} are related to each other.
|1 – 2|, |2 – 1|; |1 – 4|, |4 – 1|; |3 – 2|, |2 – 3|; |3 – 4|, |4 – 3|; |5 – 2|, |2 – 5|; |5 – 4|, |4 – 5| are not even.
So no element of {1, 3, 5} is related to any element of {2, 4}.
We hope the CBSE Sample Papers for Class 12 Maths Paper 2 help you. If you have any query regarding CBSE Sample Papers for Class 12 Maths Paper 2, drop a comment below and we will get back to you at the earliest.
