CBSE Sample Papers for Class 12 Maths Paper 1 are part of CBSE Sample Papers for Class 12 Maths. Here we have given CBSE Sample Papers for Class 12 Maths Paper 1.
CBSE Sample Papers for Class 12 Maths Paper 1
| Board | CBSE |
| Class | XII |
| Subject | Maths |
| Sample Paper Set | Paper 1 |
| Category | CBSE Sample Papers |
Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 1 of Solved CBSE Sample Paper for Class 12 Maths is given below with free PDF download solutions.
Time: 3 Hours
Maximum Marks: 100
General Instructions:
- All questions are compulsory.
- Questions 1-4 in section A are very short answer type questions carrying 1 mark each.
- Questions 5-12 in section B are short answer type questions carrying 2 marks each.
- Questions 13-23 in section C are long answer I type questions carrying 4 marks each.
- Questions 24-29 in section D are long answer II type questions carrying 6 marks each.
SECTION A
Question 1.
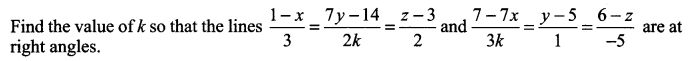
Question 2.
Evaluate \(\int { \sqrt { 1+sin2x } } dx\)
Question 3.
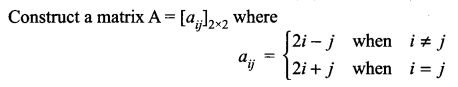
Question 4.
Find the point on the curve y = 2x2 – 6x – 5 at which tangent to the curve is parallel to x-axis.
SECTION B
Question 5.
Find mean and variance for the following probability distribution.

Question 6.
The comer points of the feasible region determined by the following system of linear inequalities 2x + y ≤ 10, x + 3y ≤ 15, x ≥ 0, y ≥ 0 are (0, 0), (5, 0), (3, 4) and (0, 5). Let Z = px + qy when p, q > 0 then find the relation between p and q so that the maximum of Z occurs at both points (3, 4) and (0, 5).
Question 7.
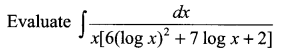
Question 8.
Matrix \(A=\left( \begin{matrix} 0 & 2b & -2 \\ 3 & 1 & 3 \\ 3a & 3 & -1 \end{matrix} \right)\) is given to be symmetric, find the value of a and b.
Question 9.
Using Rolle’s theorem, find a point on the curve y = sin x + cos x – 1, x ∈ [0, \(\frac { \pi }{ 2 }\)] tangent is parallel to x-axis.
Question 10.
If f(x) = |cos x – sin x|, find f'(\(\frac { \pi }{ 6 }\))
Question 11.
Find the coordinate of the point where the line passes through the point P(3, 4, 1) and Q(5, 1, 6) crosses the XY plane.
Question 12.
Find the intervals in which the function f(x) = log (1 + x) – \(\frac { x }{ 1+x }\) is strictly increasing.
SECTION C
Question 13.
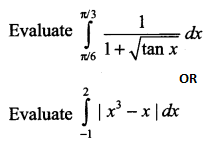
Question 14.
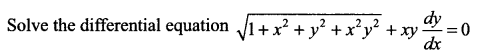
Question 15.
Using vectors find the area of the triangle with vertices A(1, 1, 2), B (2, 3, 5) and C(1, 5, 5)
OR
![]()
Question 16.
A and B throws a pair of dice turn by turn. The first to throw 9 is awarded a prize. If A starts the game, what are their respective chances of winning ? What is the importance of the game in the life of student ?
Question 17.
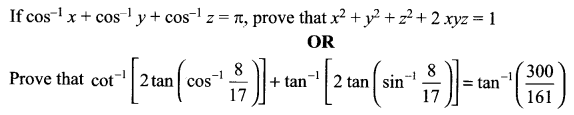
Question 18.
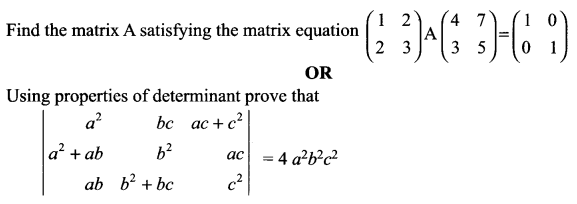
Question 19.
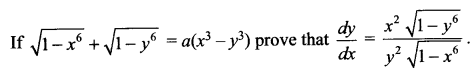
Question 20.
A pair of dice is thrown 6 times. Getting a total of 7 on the two dice is considered a success. Find the probability of getting
(i) exactly 5 successes
(ii) at most 5 successes.
Question 21.
Question 22.
Solve the following L.P.P graphically
Minimize Z = 4x + 6y
Subject to Constraints are
3x + 6y ≥ 80
4x + 3y ≥ 100
Question 23.
Evaluate \(\int { \frac { x }{ \left( { x }^{ 2 }+1 \right) \left( x+1 \right) } } dx\)
SECTION D
Question 24.
Using integration find the area of the region {(x, y): x2 + y2 ≤ 2ax, y2 ≥ ax, x, y ≥ 0}
OR
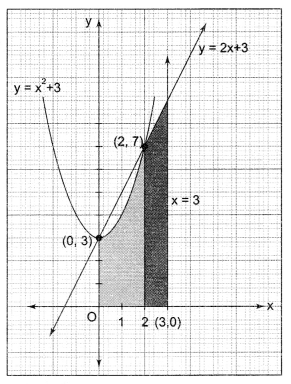
Make a rough sketch of the region given below and find its area using methods of integration.
{(x, y): 0 ≤ y ≤ x2 + 3, 0 ≤ y ≤ 2x + 3, 0 ≤ x ≤ 3}
Question 25.
Solve the following differential equation
\(\frac { dy }{ dx }\) + 2y tan x = sin x, given that y = 0 when x = \(\frac { \pi }{ 3 }\)
Question 26.
If \(A=\left( \begin{matrix} 2 & -3 & 5 \\ 3 & 2 & -4 \\ 1 & 1 & -2 \end{matrix} \right)\) find A-1 and hence solve the following system of linear equations
2x + 3y + z= 11
-3x + 2y + z = 4
5x- 4y – 2z = -9
Question 27.
Find the equation of the plane passing through the intersection of the planes 2x + 3y – z + 1 = 0 and x + y – 2z + 3 = 0 and perpendicular to the plane 3x – y – 2z – 4 = 0.
OR
Find the coordinate of the point D where the line through A (3, -4, -5) and B (2, -3, 1) crosses the plane passing through three points P(2, 2, 1), Q (3, 0, 1) and R (4, -1, 0). Also find the ratio in which D divides the line segment AB.
Question 28.
A wire of length 36 cm is cut into two pieces. One of the pieces is turned into the form of a square and the other in the form of an equilateral triangle. Find the length of each piece so that the sum of the areas of the two figures he minimum.
Question 29.
Let f : N → S be a function defined as f(x) = 4x2 + 12x + 15. Show that f: N → S where S is the range of f, is invertible. Also find the inverse of f Hence, find f-1(31).
Solutions
Solution 1.
Solution 2.
Solution 3.
Solution 4.
Solution 5.
Solution 6.

Maximum value occurs at points (3, 4) and (0, 5)
So 3p + 4q = 5q ⇒ 3p = q
Solution 7.
Solution 8.

Solution 9.
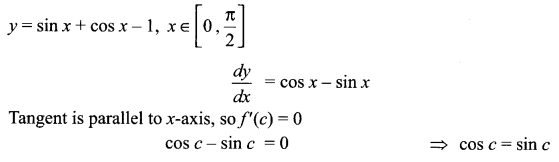
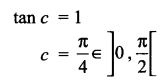
Solution 10.
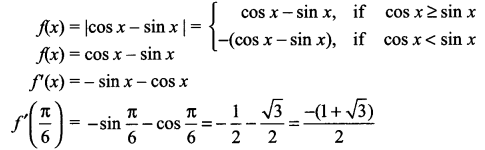
Solution 11.
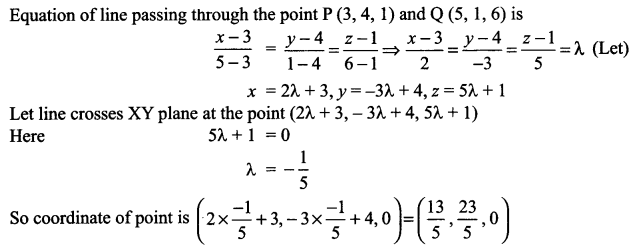
Solution 12.
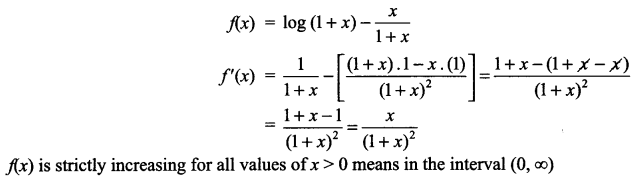
Solution 13.
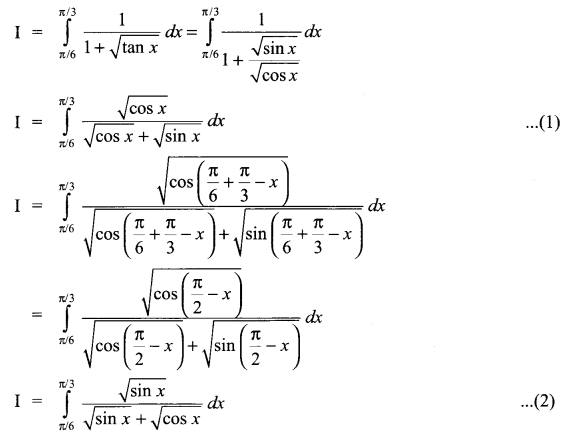

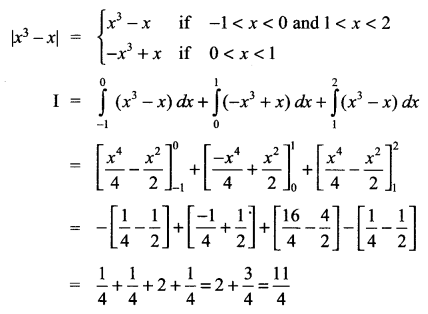
Solution 14.
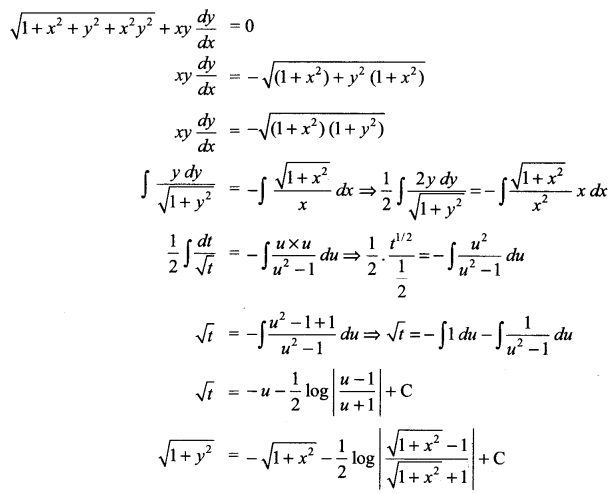
Solution 15.
A (1, 1, 2), B (2, 3, 5), C (1, 5, 5)

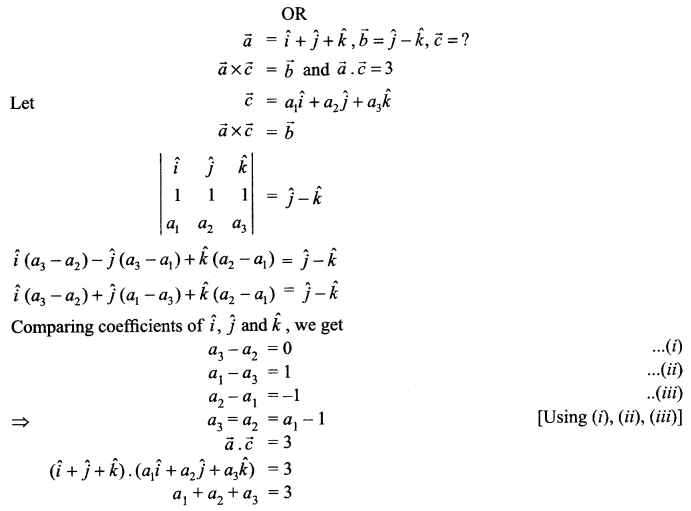
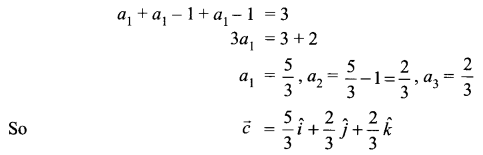
Solution 16.
When a pair of dice thrown total possible outcomes = 36

Solution 17.
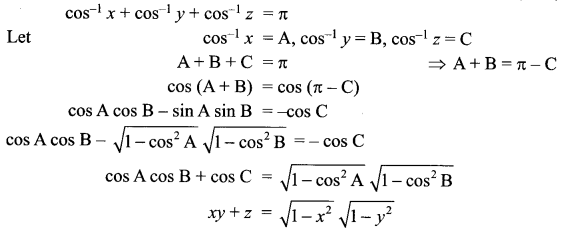

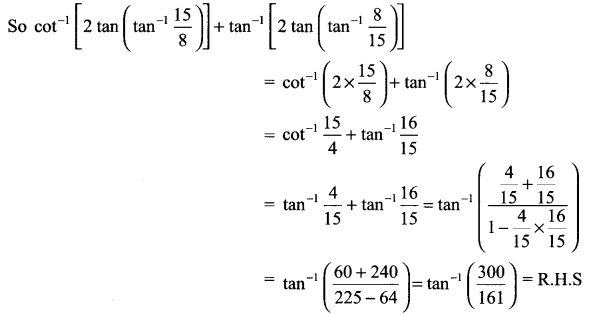
Solution 18.
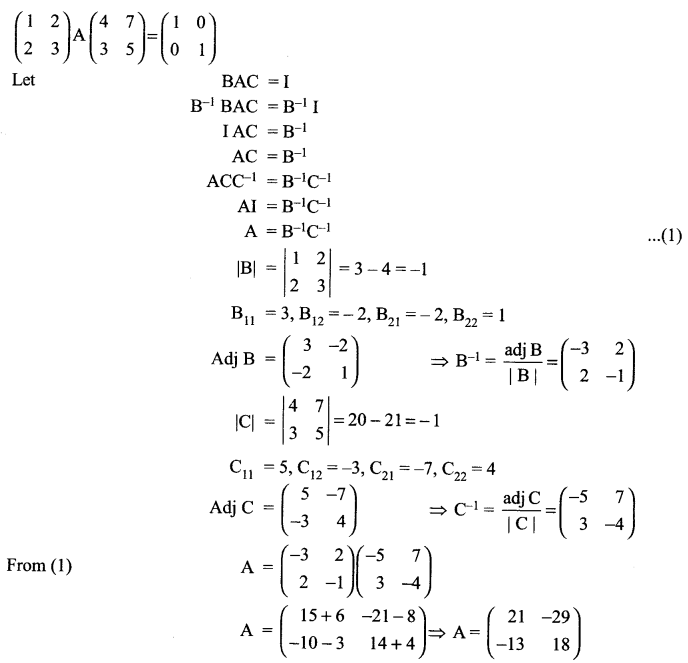

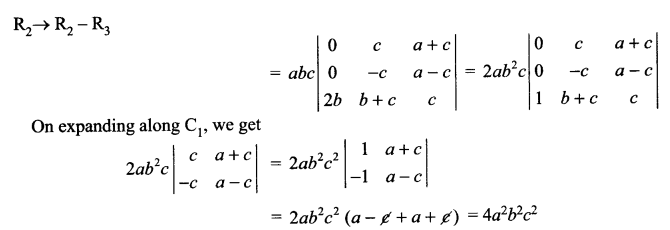
Solution 19.

Solution 20.
n = 6, total outcomes = 36
Getting a total 7 is considered a success
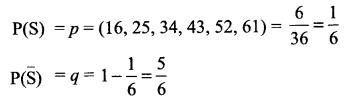
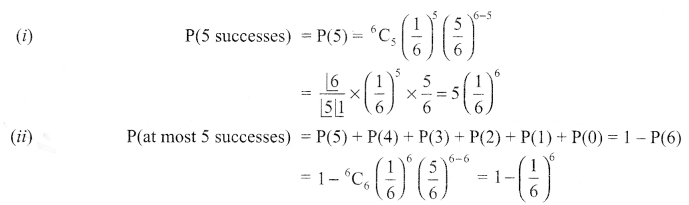
Solution 21.
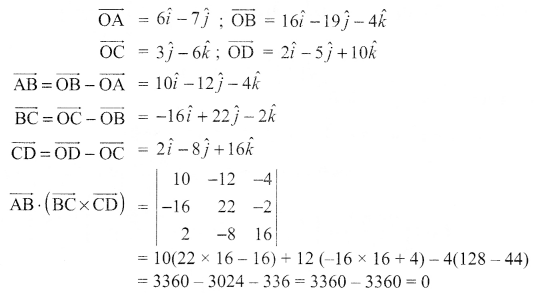
Because scalar triple product is zero, so points with given positive vectors are coplanar.
Solution 22.
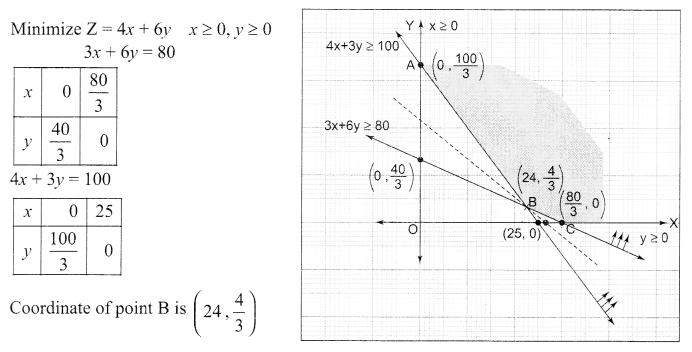

Solution 23.
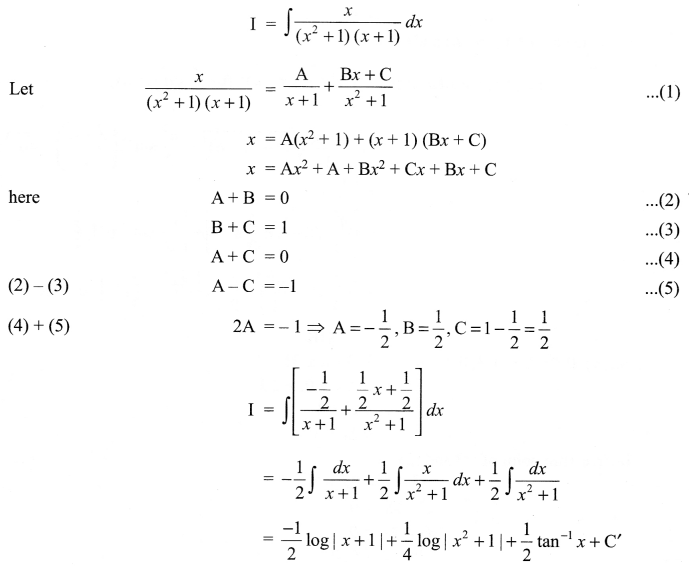
Solution 24.

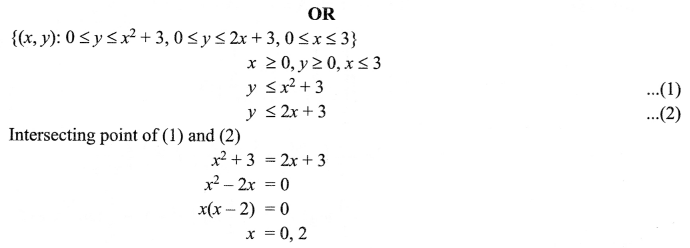

Solution 25.
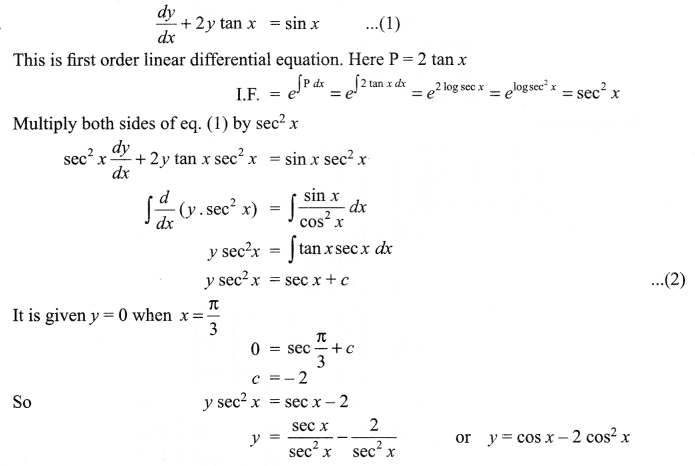
Solution 26.
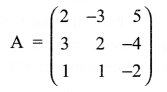
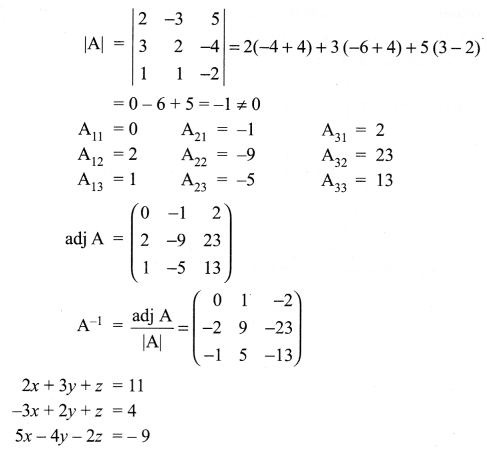
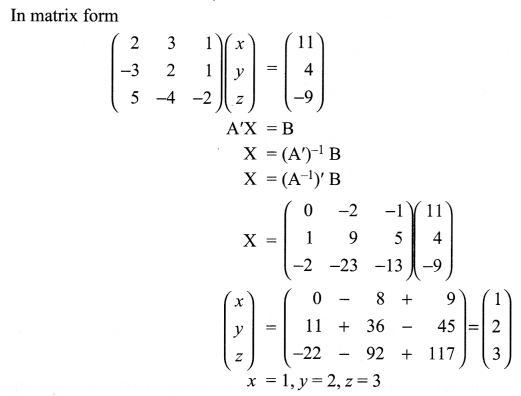
Solution 27.


Solution 28.
Let side of square is x cm and side of equilateral triangle is y cm.
Perimeter of square = 4x cm
Perimeter of equilateral triangle = 3y cm
4x + 3y = 36 (given)

Solution 29.
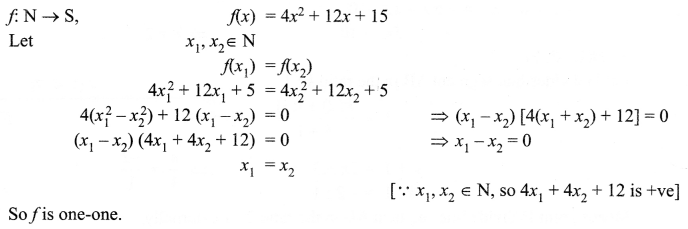

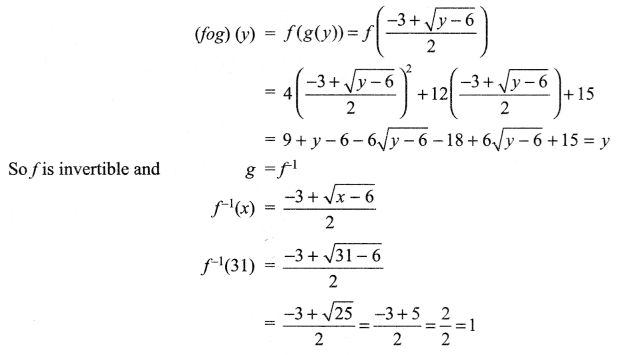
We hope the CBSE Sample Papers for Class 12 Maths Paper 1 help you. If you have any query regarding CBSE Sample Papers for Class 12 Maths Paper 1, drop a comment below and we will get back to you at the earliest.
