CBSE Class 10 Science Lab Manual - Image Formation by a Convex Lens

CBSE Class 10 Science Lab Manual – Image Formation by a Convex Lens

EXPERIMENT 8(a)

Aim
To find the image distance for varying object distances in case of a convex lens.

Materials Required
A thin convex lens, a lens holder fitted in a stand, a piece of rice paper screen fixed to a stand, a small candle with stand, a match box and a measuring scale.

Theory/Principle
The position, nature and size of the images of an object formed by a thin convex lens, depends on the position of the object and can be studied using new Cartesian sign convention and drawing ray diagrams.

Types of Images
There are two types of images :

1. Real images These are formed by the light rays which after refraction actually meet or intersect at a point or when light rays actually converge at a point. It can be obtained on the screen.
2. Virtual images These images are formed by the light rays which after refraction appear to meet at a point or appear to diverge from a point. It cannot be obtained on the screen.

Formation of Image by a Convex Lens
The table given below illustrates the ray diagrams alongwith the position and nature of image, formed by convex lens for various positions of the object.

Formation of Image by Convex Lens for Different Positions of Object

Cartesian Sign Convention
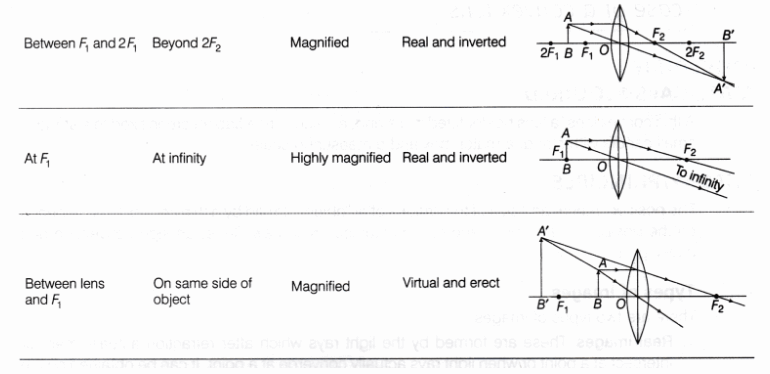
In this convention, the optical centre 0 of a convex lens LL’ is considered as the origin and its principal axis as the X-axis (X’X) of the coordinate system. The principal axis X’X is an imaginary straight line passing through two centres of curvature C₁ and C₂ of two spherical surfaces of the convex lens LL’ (as shown in Fig.1).

The optical centre 0 is a point associated with the convex lens such that a ray of light passing
through O does not suffer any deviation. Here, we consider the convex lens as a thin lens having
a small aperture, much less than its radius of curvature.
The New Cartesian sign convention can be summarised as below:

• The object is always placed to the left of the lens. This implies that the light from the object falls on the lens from the left hand side.
• All distances parallel to the principal axis are measured from the optical centre of the lens.
• All distances measured to the right of the origin along +X-axis, are taken as positive while those measured to the left of the origin along -X-axis, are taken as negative.
• Distances measured perpendicular and above the principal axis along +Y-axis, are taken as positive.
• Distances measured perpendicular and below the principal axis along -Y-axis, are taken as negative.

Thus, the nature, position and size of the image can be noted and measured from the optical centre O of a thin convex lens.

Procedure

1. Hold a thin convex lens in hand and determine its approximate focal length F by obtaining a sharp and bright image of a distant object (such as Sun or distant tree) on a wall and measuring the distance between the image and lens.
2. Fix the thin convex lens on a lens holder and place it vertically near the middle of the tabie.
3. Note down the position (l) of the thin convex lens in the observation table.
4. Place the semi-transparent rice paper screen, fitted to a stand on the other side of the lens.
5. Mount a small candle in a centred mark stand vertically and light it.
6. Adjust the height of the centre of lens nearly equal to the height of the flame of the candle. Here the candle flame is considered as the object AB. Measure and record the height h of the candle flame.
   
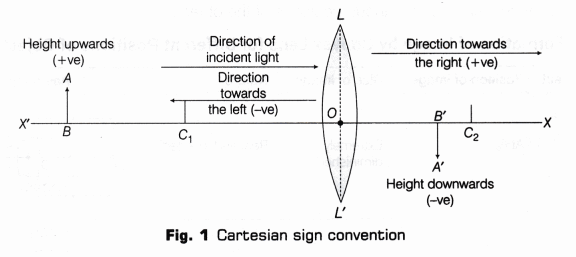
7. Place the lighted candle flame in front of convex lens beyond the twice of the aproximate focal length, i.e. beyond the centre of curvature (2F) of convex lens as shown in Fig. 2.
8. Note down the position of lighted candle (c). Find the distance, x (say) between the optical centre O of the lens and candle flame (object).
9. Locate a sharp image A’B’ of the candle flame AB in the convex lens from the other side of the lens, adjusting the position of the screen.
10. Note down the position of screen, s. Find the distance between optical centre O of the lens and the screen, y (say). Also, measure and record the height h’ of the image of the candle flame obtained on the screen.
11. Now shift the lighted candle nearby but beyond, 2F of convex lens. Note down and record the position of lighted candle AB (c) and lens (l).
12. Adjust the position of the screen by moving it away from the previous position to get a real and sharp image A’B’ of the candle flame AB. Note down the position of screen, s. Find the distance y and record the height h’ of image of candle flame obtained on the screen.
13. Repeat the experiment by shifting the candle in front of convex lens at a distance:
    • Equal to 2F
    • Less than 2F but more than F
      Obtain the real and sharp image of the candle flame on the screen in each case by moving it further away from lens and record your observations.
14. Now place the lighted candle at F and try to locate the image on screen by moving it gradually away from the lens. You may not be able to obtain the image because it will be formed at infinity and is blurred due to high magnification.
15. Record all the observations in the corresponding observation table.

Observations and Calculations

1. Approximate focal length of thin convex lens, f = …………… cm
2. Height of candle flame, h = ………….. cm

Result
The image distances for varying object distances in case of convex lens is given below:

PrecautionsIt is clearly visible from the above table as the object is movqd from infinity towards the optical centre of thin convex lens, the image distance increases gradually and height of image also increases gradually.

1. A thin convex lens, having small aperture should be used to perform the experiment.
2. The base of the stands of the convex lens and screen should be parallel to the measuring scaie.
3. For obtaining distinct and sharp images of candle flame, perform this experiment in a dark room.
4. The flame of candle should be uniform throughout the experiment. To avoid its flickering, perform the experiment in calm air and switch OFF the fan.
5. While finding out the approximate value of focal length F of convex lens by using Sun as an object, do not look at the image directly with the naked eyes, otherwise it may damage-the eyes.’
6. The focal length of thin convex lens should be preferably between 15 to 20 cm.

Sources of Error

1. The convex lens may be thick and may have scratches.
2. The centre of lens, centre of stand of candle flame and centre of screen, may not be in same straight line and parallel to measuring scale.
3. The experiment may not be performed in a dark room.
4. Flame may not be uniform throughout the experiment.

Viva – Voce

Question 1.
A distinct image of the lighted candle has been obtained on the screen with fixed position using a thin convex lens. Why does the image of the candle get blurred, if the position of any one of them is slightly disturbed? [NCERT]
Answer:
As we change the position of the object or lens, the image formed will be blurred, it is due to the rays which may meet before or after the screen.

Question 2.
Why do we require a calm atmosphere to perform this experiment? [NCERT]
Answer:
We require a calm atmosphere so that flame becomes uniform throughout the experiment. Because it is difficult to measure flame height as well as image height of flickering plasma.

Question 3.
Why is it preferred to perform this experiment in dark or shade? [NCERT]
Answer:
To get sharp and distinct image of the candle flame, it is preferred to perform this experiment in dark or shade.

Question 4.
How will you distinguish between a convex lens and a concave lens by holding in hand and looking the printed page through them? [NCERT]
Answer:
As concave lens cannot form enlarged image at any position of lens, so the lens which will form enlarged image of printed page, will be a convex lens.

Question 5.
What effect do you expect if the lens is thick? [NCERT]
Answer:
Thick convex lens has shorter focal length so image distance will be reduced as compared to thin lens.

Question 6.
What effect do you expect if the lens used to perform the experiment has scratches on it?
Answer:
A sharp and distinct image will not be obtained accurately.

Question 7.
What is the nature of focal length of convex lens according to New Cartesian sign convention?
Answer:
The focal length of convex lens is positive.

Question 8.
What will be the nature of image obtained on screen if a lower half of convex lens is covered with black paper?
Answer:
The full size image will be obtained but with reduced brightness.

Question 9.
On what factor does the size of an image formed by a thin convex lens depend?
Answer:
The size of an image depends on the position of an object from the lens.

EXPERIMENT 8(b)

Aim
To draw the ray diagrams to show the nature of the image formed by a convex lens when object is placed at various positions.

Materials Required
Sheets of white paper, a drawing board, measuring scale, protractor, a sharp pencil and drawing pins or adhesive tape.

Theory/Principle
The light rays when refracted through a convex lens obey laws of refraction. The formation of images by a convex lens can be studied by drawing ray diagrams and by following New Cartesian sign convention.
For an illuminated extended object AB of finite size, placed in front of a convex lens, its each small portion acts like a point source of light. An infinite number of rays of light come from each of these point sources which could be considered for drawing the ray diagrams in order to locate the image of an object, formed by a convex lens.
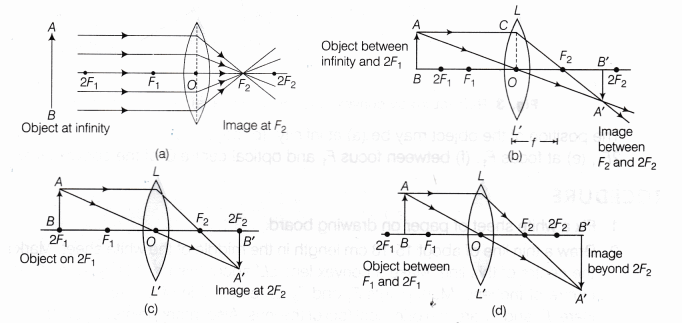
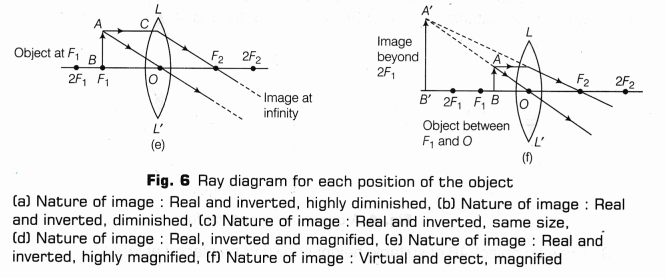
For drawing ray diagrams for convex lens, we consider any two of the following three rays.

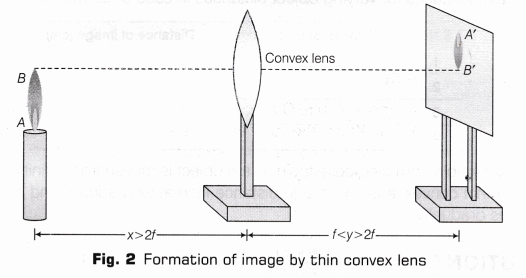
• A ray of light from the object, parallel to the principal axis, after refraction from a convex lens, passes through the principal focus F₂ on the other side of the lens as given in the Fig. 1.
  
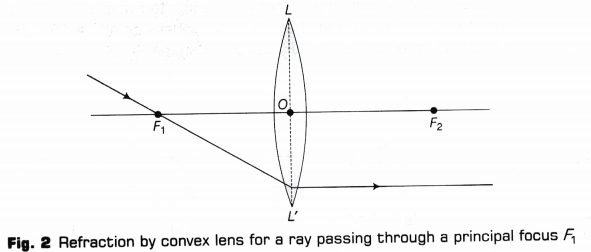
• A ray of light passing through a principal focus F₁ after refraction from a convex lens, will emerge parallel to the principal axis as given in Fig. 2.
  
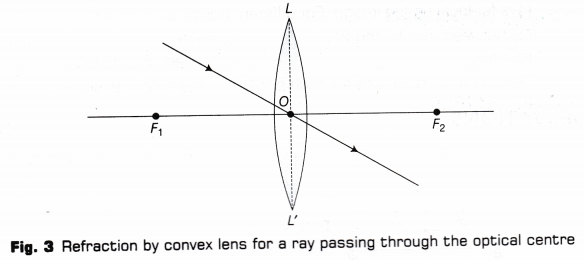
• A ray of light passing through the optical centre 0 of a convex lens will not suffer any deviation as given in Fig. 3.
  
  The position of the object may be (a) at infinity, (b) beyond 2F₁, (c) at 2F₁, (d) between
  F₁ and 2F₁, (e) at focus F₁ (f) between focus F₁ and optical centre O of the convex lens.

Procedure

1. Fix a white sheet of paper on drawing board.
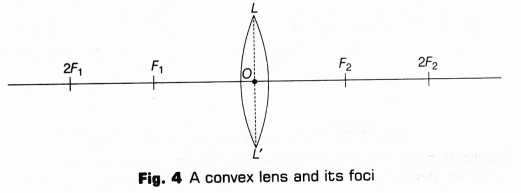
2. Draw a thin line of about 15-18 cm length in the middle of the white sheet. Mark a point O at the centre of this line. Make a convex lens LL’ about this point O. Assume 0 as the optical centre of the lens. Mark points F₁ and F₂ on either side of the lens, such that, OF₁ = OF₂. Here.F₁ andF₂ are two prinicipal foci of the lens. Also, mark points 2F₁ and 2F₂ on the line at double the distances OF₁ and OF₂ as given in the Fig. 4.
   
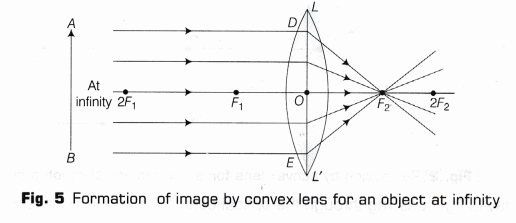
3. Draw an object AB of suitable height shown to be placed at infinity.
4. Draw thin lines, representing incident rays coming from the object AB parallel to the principal axis F₁OF₂ , striking the surface of the convex lens LL’ at the points of incidence D, E etc. These rays after refraction emerge as refracted rays DF₂, FF₂ and so on. These rays intersect at the focus F₂ of the lens on the other side and a diminished image of the distant object is formed at the point F₂ , as shown in the Fig. 5.
   
5. Repeat the above steps, using the New Cartesian sign convention and considering relevant rays for locating the image. For different positions of object
   • between infinity and 2F₁
   • on 2F₁
   • between 2F₁ and F₁
   • on F₁
   • between F₁ and lens
     Draw neat ray diagrams for each position of the object as shown in observations.

Observations

Result
The ray diagrams to show the nature of image formed by a convex lens when object is placed at various positions is shown in Fig. 6.
In the case when object is placed anywhere between infinity and focus, the image will be real and inverted. And in case if object is placed between F and O, it will be virtual and erect.

Precautions

1. The convex lens should be thin and of small aperture for obtaining the distinct image.
2. Use a very sharp tipped pencil to draw thin lines to represent incident and refracted rays.

Sources of Error

1. Pencil may not be too sharp.
2. Measuring scale may not be placed in straight line.

Viva-Voce

Question 1.
Sometimes the image formed by a convex lens of an object placed at 2F₁ is not of the same size and at location 2F₂ on the other side of the convex lens. What could be the possible reasons for such a situation? [NCERT]
Answer:
If the lens is thick and having larger aperture, then it will not form image at the given location.

Question 2.
A ray of light is passing through the principal focus of a convex lens. How will it emerge after refraction through the lens? [NCERT]
Answer:
When a light ray passes through principal focus after refraction, it will be parallel to the principal axis.

Question 3.
An object is placed on the left side of a lens (of focal length 10 cm) at a distance of 20 cm. What will be the sign of object distance? [NCERT]
Answer:
As in the theory of this experiment, we find that according to New Cartesian sign convention, the sign of object distance will be negative.

Question 4.
Which laws of light are obeyed by the light rays when refracted through a convex lens?
Answer:
Laws of refraction of light are obeyed by light rays when refracted through a convex lens.

Question 5.
A student draws a ray diagram for image formation by a convex lens for an object placed at 2F. What will be the magnification produced by convex lens in this case?
Answer:
The magnification will be +1.

Question 6.
Why do we draw equiconvex lens to show the image formation by it?
Answer:
If we do not draw an equiconvex lens, then the condition OF₁ = OF₂ will not hold good and the image obtained will not be accurate.

Question 7.
Which of the quantity remains same when light travels from one medium to another medium?
Answer:
Frequency of light.

Question 8.
Will virtual image formed by convex lens be erect or inverted?
Answer:
The virtual image will always be erect.

Question 9.
How many rays are required to draw the ray diagram to show the image formation by lens? Why?
Answer:
Two rays are required to draw the ray diagram. It is because

• of sake ofclearity of ray diagram
• to know their directions after refraction from the lens.

Question 10.
If a ray of light does not suffer any deviation from the path of incidence after refraction, what will you say?
Answer:
It means that the ray passes through the optical centre of the lens.

Question 11.
What happens to the size of image when object is moved from infinity to a point closer to optical centre of the convex lens?
Answer:
The size of the image increases gradually.

Question 12.
A student was asked to draw a ray diagram for image formation of an object placed at a distance of 3 cm from a convex lens of focal length 4 cm. What will be the nature of the image formed after completing the diagram?
Answer:
A virtual, erect and magnified image will be formed.

Question 13.
What will be the nature and position of image formed by a convex lens, when the object is placed between F₁ and 2F₁?
Answer:
If an object is placed between F₁ and 2F₁ then a real, inverted and enlarged image will be formed beyond 2F₂.

Science Lab ManualScience Practical SkillsScience LabsMath LabsMath Labs with Activity