Bisect a Line Segment and an Angle
Bisect – cut into two congruent (equal) pieces.
Bisect a line segment
(Also known as Construct a Perpendicular Bisector of a segment)
Given: (Line segment) \(\overline { AB }\).
![]()
Task: Bisect \(\overline { AB }\)
Directions:
- Place your compass point on A and stretch the compass MORE THAN half way to point B, but not beyond B.
- With this length, swing a large arc that will go BOTH above and below \(\overline { AB }\).
(If you do not wish to make one large continuous arc, you may simply place one small arc above \(\overline { AB }\) and one small arc below \(\overline { AB }\).)
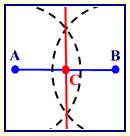
- Without changing the span on the compass, place the compass point on B and swing the arc again. The two arcs you have created should intersect.
- With your straightedge, connect the two points of intersection.
- This new straight line bisects \(\overline { AB }\). Label the point where the new line and \(\overline { AB }\) cross as C.
\(\overline { AB }\) has now been bisected and AC = CB. (It could also be said that the segments are congruent, \(\overline { AC } \cong \overline { CB }\).)
(It may be advantageous to instruct students in the use of the “large arc method” because it creates a “crayfish” looking creature which students easily remember and which reinforces the circle concept needed in the explanation of the construction.)
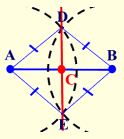
Explanation of construction: To understand the explanation you will need to label the point of intersection of the arcs above segment \(\overline { AB }\) as D and below segment \(\overline { AB }\) as E. Draw segments \(\overline { AD }\), \(\overline { AE }\), \(\overline { BD }\) and \(\overline { BE }\). All four of these segments are of the same length since they are radii of two congruent circles. More specifically, DA = DB and EA = EB. Now, remember a locus theorem: The locus of points equidistant from two points, is the perpendicular bisector of the line segment determined by the two points. Hence, \(\overline { DE }\) is the perpendicular bisector of \(\overline { AB }\).
The fact that the bisector is also perpendicular to the segment is actually MORE than we needed for a simple “bisect” construction.
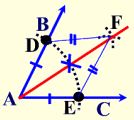
Bisect an angle
Given: ∢BAC
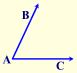
Task: Bisect ∢BAC.
Directions:
- Place the point of the compass on the vertex of ∢BAC (point A).
- Stretch the compass to any length so long as it stays ON the angle.
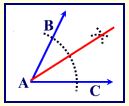
- Swing an arc so the pencil crosses both sides of ∢BAC. This will create two intersection points with the sides (rays) of the angle.
- Place the compass point on one of these new intersection points on the sides of ∢BAC.
If needed, stretch your compass to a sufficient length to place your pencil well into the interior of the angle. Stay between the sides (rays) of the angle. Place an arc in this interior – you do not need to cross the sides of the angle. - Without changing the width of the compass, place the point of the compass on the other intersection point on the side of the angle and make the same arc. Your two small arcs in the interior of the angle should be crossing.
- Connect the point where the two small arcs cross to the vertex A of the angle.
You have now created two new angles that are of equal measure (and are each 1/2 the measure of ∢BAC.)
Explanation of construction: To understand the explanation, some additional labeling will be needed. Label the point where the arc crosses side \(\overline { AB }\) as D. Label the point where the arc crosses side \(\overline { AC }\) as E. And label the intersection of the two small arcs in the interior as F. Draw segments \(\overline { DF }\) and \(\overline { EF }\). By the construction, AD = AE (radii of same circle) and DF = EF (arcs of equal length). Of course AF = AF. All of these sets of equal length segments are also congruent. We have congruent triangles by SSS. Since the triangles are congruent, any of their leftover corresponding parts are congruent which makes ∢BAF equal (or congruent) to ∢CAF.