Binomial Theorem for any Index
Binomial theorem for positive integral index
The rule by which any power of binomial can be expanded is called the binomial theorem.
If n is a positive integer and x, y ∈ C then
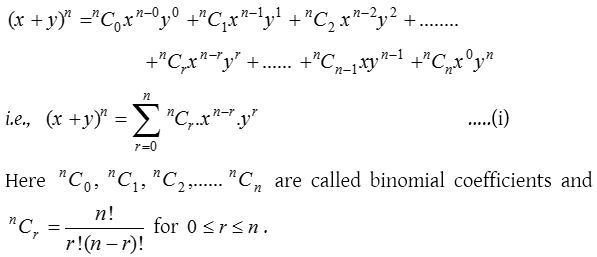
Binomial theorem for any Index
Statement :
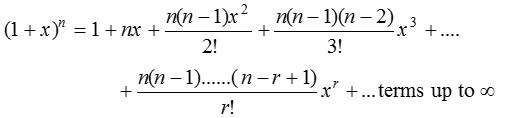
when n is a negative integer or a fraction, where , otherwise expansion will not be possible.
If first term is not 1, then make first term unity in the following way,
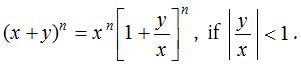
General term :
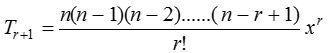
Some important expansions
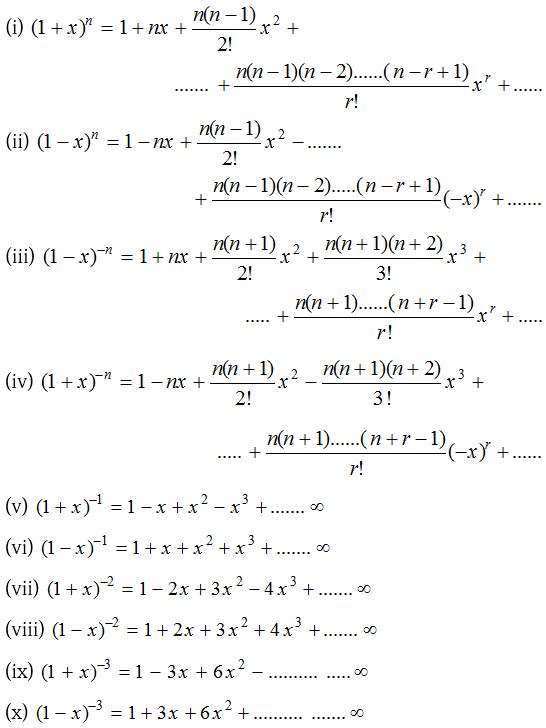
Problems on approximation by the binomial theorem :
We have,
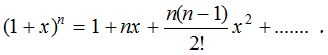
If x is small compared with 1, we find that the values of x2, x3, x4, ….. become smaller and smaller.
∴ The terms in the above expansion become smaller and smaller. If x is very small compared with 1, we might take 1 as a first approximation to the value of (1 + x)n or (1 + nx) as a second approximation.
Three / Four consecutive terms or Coefficients
(1) If consecutive coefficients are given: In this case divide consecutive coefficients pair wise. We get equations and then solve them.
Some important points
(1) Pascal’s Triangle
Pascal’s triangle gives the direct binomial coefficients.
Example : (x + y)4 = x4 + 4x3y + 6x2y2 + 4xy3 + y4.
(2) Method for finding terms free from radicals or rational terms in the expansion of (a1/p + b1/q)N ∀ a, b ∈ prime numbers:
Find the general term
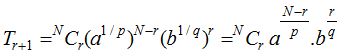
Putting the values of 0 ≤ r ≤ N, when indices of a and b are integers.
Number of irrational terms = Total terms – Number of rational terms.