Binomial Probability “At Least / At Most”
When computing “at least” and “at most” probabilities, it is necessary to consider, in addition to the given probability,
• all probabilities larger than the given probability (“at least”)
• all probabilities smaller than the given probability (“at most”)
The probability of an event, p, occurring exactly r times:
n Cr .pr . qn-r
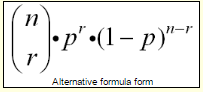
n = number of trials
r = number of specific events you wish to obtain
p = probability that the event will occur
q = probability that the event will not occur
(q = 1 – p, the complement of the event)
Illustration:
A bag contains 6 red Bingo chips, 4 blue Bingo chips, and 7 white Bingo chips.
What is the probability of drawing a red Bingo chip at least 3 out of 5 times?
Round answer to the nearest hundredth.
To solve this problem, we need to find the probabilities that r could be 3 or 4 or 5, to satisfy the condition “at least”.

Examples: (answers rounded to the nearest hundredth)
1. A family consists of 3 children. What is the probability that at most 2 of the children are boys?
Solution:
“At most” 2 boys implies that there could be 0, 1, or 2 boys. The probability of a boy child (or a girl child) is 1/2.

2. Team A and Team B are playing in a league. They will play each other five times. If the probability that team A wins a game is 1/3, what is the probability that team A will win at least three of the five games?
Solution:
“At least” 3 wins implies 3, 4, or 5 wins.

