What is Arithmetico–Geometric Sequence?

What is Arithmetico–Geometric Sequence?

https://www.youtube.com/watch?v=5L0HvXfmNsA

Arithmetico-geometric Progression (A.G.P.)

Definition:
The combination of arithmetic and geometric progression is called arithmetico-geometric progression.

n^th term of A.G.P.

If a₁, a₂, a₃, ……. a_n, ..…. is an A.P. and b₁, b₂, b₃, ……. b_n, ..…. is a G.P., then the sequence a₁b₁, a₂b₂, a₃b₃, …….., a_nb_n, …….. is said to be an arithmetico-geometric sequence.
Thus, the general form of an arithmetico geometric sequence is a, (a + d)r, (a + 2d)r², (a + 3d)r³, ………
From the symmetry we obtain that the n^th term of this sequence is [a + (n – 1)d]r^n–1.
Also, let a, (a + d)r, (a + 2d)r², (a + 3d)r³, ……… be an arithmetico-geometric sequence.
Then, a, (a + d)r, (a + 2d)r², (a + 3d)r³, ……… is an arithmetico-geometric series.

Sum of A.G.P.

Method for finding sum

This method is applicable for both sum of n terms and sum of infinite number of terms.
First suppose that sum of the series is S, then multiply it by common ratio of the G.P. and subtract. In this way, we shall get a G.P., whose sum can be easily obtained.

Method of difference

If the differences of the successive terms of a series are in A.P. or G.P., we can find n^th term of the series by the following steps :
Step I: Denote the n^th term by T_n and the sum of the series upto n terms by S_n.
Step II: Rewrite the given series with each term shifted by one place to the right.
Step III: By subtracting the later series from the former, find T_n.
Step IV: From T_n, S_n can be found by appropriate summation.

Example : Consider the series 1+ 3 + 6 + 10 + 15 +…..to n terms. Here differences between the successive terms are 3 – 1, 6 – 3, 10 – 6, 15 – 10, …….i.e., 2, 3, 4, 5,…… which are in A.P. This difference could be in G.P. also. Now let us find its sum:

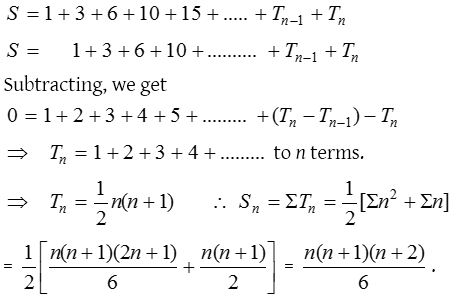
Miscellaneous series

Special series

(1) Sum of first n natural numbers

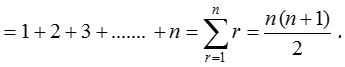
(2) Sum of squares of first n natural numbers

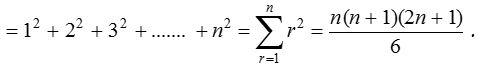
(3) Sum of cubes of first n natural numbers