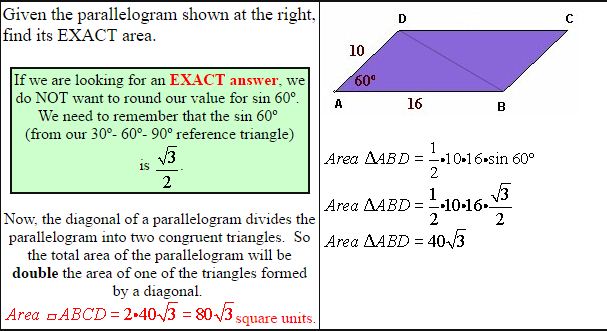
Area of Triangle and Parallelogram Using Trigonometry
We are all familiar with the formula for the area of a triangle, A = 1/2 bh , where b stands for the base and h stands for the height drawn to that base.
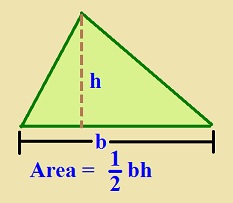
In the triangle shown below, the area could be expressed as: A= 1/2ah

Now, let’s be a bit more creative and look at the diagram again. By using the right triangle on the left side of the diagram, and our knowledge of trigonometry, we can state that: Sin c =h/b
b Sin c = h
This tells us that the height, h, can be expressed as b sinC.
If we substitute this new expression for the height, we can write the triangle area formula as: A = 1/2 ab Sin C
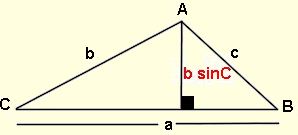
We have just discovered that the area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. This is often referred to as the SAS Formula for the area of a triangle.
The “letters” in the formula may change from problem to problem, so try to remember the pattern of “two sides and the sine of the included angle”.
“Wow! A trig area formula for triangles!!!”
We no longer have to rely on a problem supplying us with the length of the altitude (height) of the triangle in order for us to find the area of the triangle. If we know two sides and the included angle, we are in business.
Read More:
- Angle Sum Property of a Triangle
- Median and Altitude of a Triangle
- The Angle of An Isosceles Triangle
- Areas of Two Similar Triangles
- Area of A Triangle
- To Prove Triangles Are Congruent
- Criteria For Similarity of Triangles
- Construction of an Equilateral Triangle
Example 1:
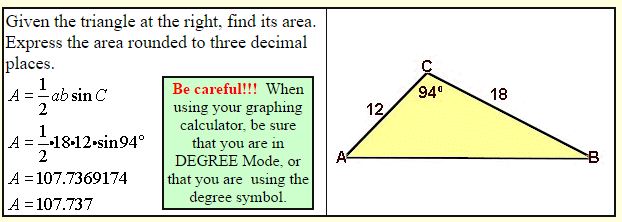
Example 2: