Arc Length and Radian Measure

(The arc length discussed on this page will be in relation to a circle.)
An arc of a circle is a “portion” of the circumference of the circle.
The length of an arc is simply the length of its “portion” of the circumference. Actually, the circumference itself can be considered an arc length.
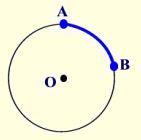
The length of an arc (or arc length) is traditionally symbolized by s.

In the diagram at the right, it can be said that ” AB subtends angle θ “.
Definition: subtend – to be opposite to
Radian Measure

The radian measure θ of a central angle of a circle is defined as the ratio of the length of the arc the angle subtends, s, divided by the radius of the circle, r.
θ = s/r = length of subtended arc / length of radius


Relationship between Degrees and Radians:

