How is apparent depth and real depth related to refractive index?

Figure shows two opaque cups, A and B. Cup A is partially filled with water and cup B is totally filled with water. A similar coin is placed at the bottom of each cup.
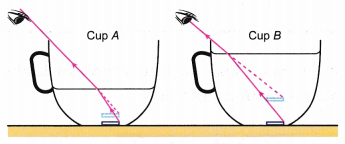
When observing from the same position, the coin in cup A cannot be seen, but the coin in cup B can be seen.
With more water in the cup, the image of the coin in cup B is actually at a higher position than that in cup A. This made the coin, which cannot be seen in cup A, visible in cup B without adjusting the position of the eye.
This shows that the position of an image depends on the depth of the water.
Figure shows how a coin in the water is seen by an observer. This effect is caused by the refraction at the surface of the water.
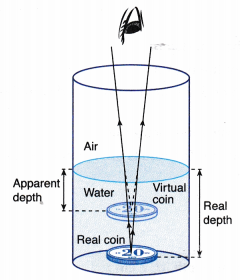
Rays of light coming from the coin are bent away from the normal as they leave the water.
When they reach the eye, they appear to come from a virtual coin, which is above the real coin.
The apparent depth is the distance of the virtual image, I from the surface of the water.
The real depth is the distance of the real object, O from the surface of the water.
The relation of refractive index, n to real depth and apparent depth is given by:

People also ask

Real and Apparent Depth Experiment

Aim: To find the relationship between the real depth and the apparent depth of an object placed in water.
Problem: How does the apparent depth of an object in water vary with its real depth?
Hypothesis: When the real depth of an object in water increases, its apparent depth also increases. Variables:
(a) Manipulated variable: Real depth, d₁
(b) Responding variable: Apparent depth, d₂
(c) Fixed variable: The density of water
Materials: 2 steel pins, 1 cork, jug of water
Apparatus: Tall beaker, metre rule, retort stand
Method:

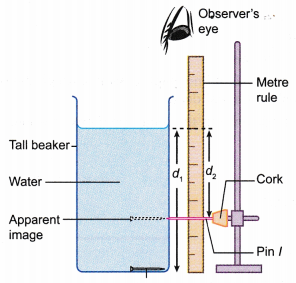
apparent depth and real depth 2

The apparatus is set up as shown in Figure.
A steel pin (Pin O) is placed at the bottom of the tall beaker.
The other steel pin is fixed on a cork that is held by the clamp of a retort stand. It is used as a search pin (Pin l).
The tall beaker is filled with water to a height of d₁ = 20 cm (the real depth).
The image of the steel pin is viewed vertically above the edge of the beaker.
The search pin which is adjacent to the beaker is then moved up or down until it is levelled with the image of the steel pin seen through the water.
The position of the image, d₂ (the apparent depth) is measured using the metre rule.
Steps 4 to 7 are repeated with d₁ = 30 cm, 40 cm, 50 cm and 60 cm. The results are recorded in Table.
A graph of real depth (d₁) against apparent depth (d₂) is plotted.

Results:
1. Tabulation of results.

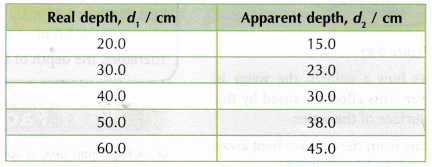
apparent depth and real depth 3

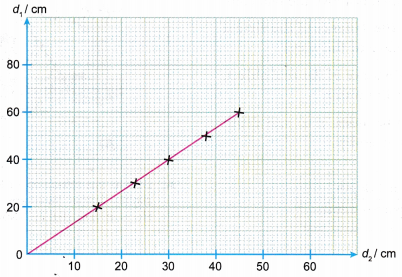
2. Graph of real depth (d₁) against apparent depth (d₂).

apparent depth and real depth 4

Discussion:

The apparent depth is always smaller than the real depth.
When the real depth increases, the apparent depth also increases.
The graph of real depth d₁ against the apparent depth d₂ is a straight line graph passing through the origin. This shows that the apparent depth is directly proportional to the real depth.
The gradient of the graph of real depth d₁ against apparent depth d₂ is the refractive index of water.

Conclusions:

The results of the experiment support the hypothesis.
The ratio of Real depth to Apparent depth is the refractive index of water.

Real and Apparent Depth Problems

A fish at the bottom of a pond appears to be 1.2 m from the water surface. What is the depth of the pond?
[Refractive index of water = 1.33]
Solution:
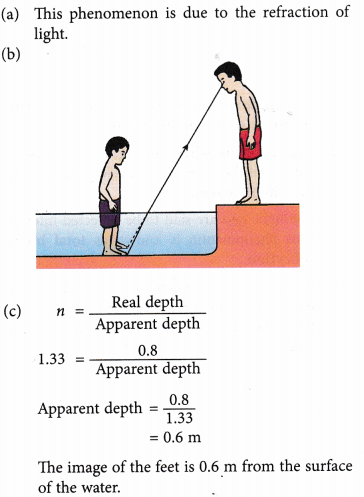
Figure shows a boy standing inside a swimming pool. His legs appear shorter when his friend observes him from the pool side.

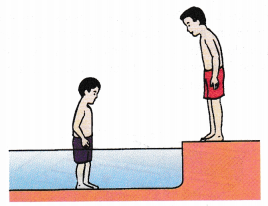
(a) Explain how this phenomenon occurs.
(b) Draw a ray diagram to show how his legs appear shorter.
(c) If the depth of the pool is 0.8 m, calculate the distance of the image of his feet as seen from the surface of the water.
[Refractive index of water = 1.33]
Solution: