Angle Sum and Difference, Double Angle and Half Angle Formulas
Hipparchus, considered to be the most eminent of Greek astronomers (born 160 B.C.),
derived the formulas for
The following formulas (or formulae, in Latin) are trigonometric identities.
Sum and Difference Formulas:
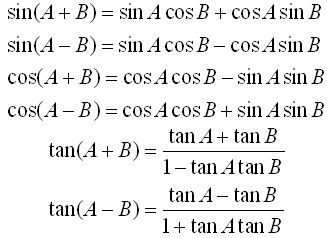
Double Angle Formulas:
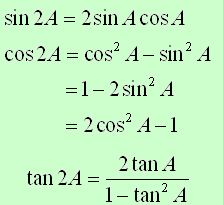
Half Angle Formulas
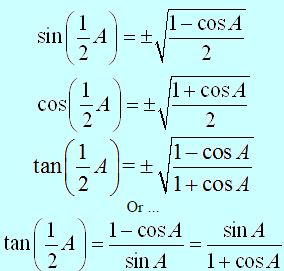
Example 1:
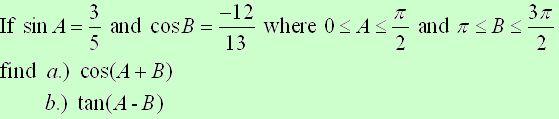
Solution: The given information produces the triangles shown at the right. The Pythagorean Theorem, or a Pythagorean triple, is used to find the missing sides. Using the information from the triangles, find the answers to parts a and b.
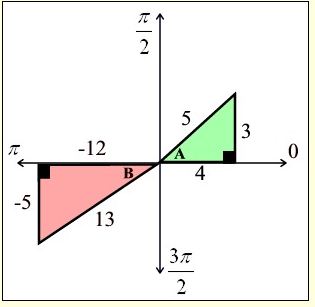
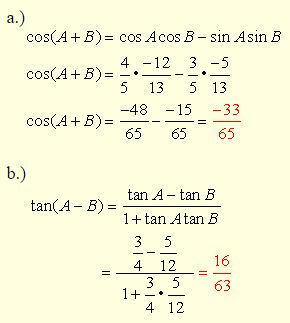

Example 2:
Using the half angle formula, find the exact value of cos 15º.
Solution:
The positive square root is chosen because cos 15º lies in Quadrant I.
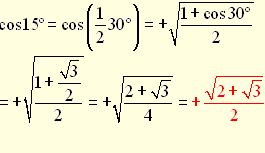
Example 3:

