Algebraic Translations
In the lesson on Algebraic Representations we looked at writing mathematical expressions.
We are ready now to write mathematical equations.
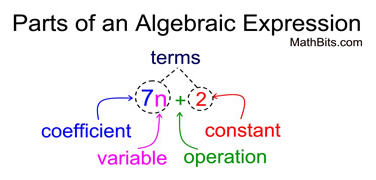
The word “terms” refers to values that are added or subtracted. 7n + 2 has two terms.
The word “factors” refers to values that are multiplied. The term 7n has two factors: 7 and n.
“Expressions” and “equations” refer to two different entities in mathematics.
If you are dealing with an EQUAL SIGN, you are dealing with an “equation”.
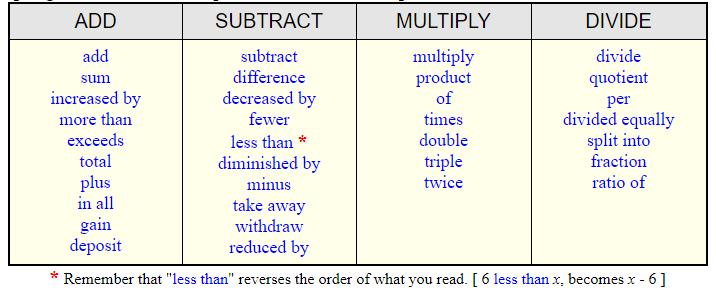
The skill of translating between verbal statements and algebraic expressions requires an understanding of the words that are commonly used to represent mathematical operations.
A sampling of words used to represent mathematical operations:
Examples
Translate the following problems into equations:
HINT: If you are having trouble determining what the equation might be, make a numerical problem to see how the numbers in the problem are related to one another.
| 1. | Cost for cable TV service in a certain city is $45 for the installation and $24 a month for service. Number problem: for 3 months the cost would be: Cost = $24 • 3 + $45. Replace 3 with m. | Let c = cost, m = number of months c = 24m + 45 |
| 2. | If golf balls cost $1.25 and putters cost $79, how many of each can the golf team purchase for $150? Number problem: if I purchase 2 golf balls and 3 putters the cost will be: Cost = 1.25•2 + 79•3 Replace 2 with g (number of golf balls), 3 with p(number of putters), and Cost with $150. | Let g = number of golf ball, p = number of putters 1.25g + 79p = 150 |
| 3. | H2O means that water contains two hydrogen atoms and one oxygen atom. Number problem: In water, if there is one oxygen atom, there are 2 hydrogen atoms; if there are two oxygen atoms, there are 4 hydrogen atoms and so on. The number of hydrogen atoms is twice the number of oxygen atoms. | Let O = number of oxygen atoms, H = number of hydrogen atoms H = 2O |
| 4. | A cookie recipe calls for twice as many chocolate chips as walnuts. Number problem: if a recipe calls for 10 walnuts, it calls for 20 chocolate chips. The number of chocolate chips is twice the number of walnuts. | Let c = number of chips, w = number of walnuts c = 2w |
| 5. | What is the total weight of a filled hot tub, if the tub weighs 350 pounds and the water weighs 10 pounds per gallon? Number problem: if it takes 100 gallons to fill the hot tub, the total weight will be: Total = 10 • 100 + 350 Replace 100 with g, for the number of gallons. | Let t = total weight, g = number of gallons t = 10g + 350 |
