Algebraic Expression

Any combination of literal numbers or variables and numbers (numerals) connected by +, –, × or ÷ signs is called an algebraic expression.
For example,
5, 6x, a + b × c, 4 × m + n, x – y ÷ z are algebraic expressions. The perimeter P of a triangle whose sides are a, b and c is given by P = a + b + c, area of square is x × x i.e., x² are algebraic expressions.
A repeated product of a number with itself is written in exponential form.
2 × 2 × 2 × 2 = 2⁴, etc
The same is true for literal numbers also. Thus, if x is a literal, then we have
x × x × x = x³ (Third power of x or x cube)
x × x × x × x = x⁴ and so on.
Also, 7 × x × x = 7x²
4 × x × x × y × y = 4x² y², etc.
x × x × x ……, n times = xⁿ and read as n-th power of x. Here x is called base and n, exponent.

For example :

Algebraic Expression	No. of terms	Terms
(i) –32x	1	–32x
(ii) 2x + 3y	2	2x and 3y
(iii) ax – 5y + cz	3	ax, –5y and cz
(iv) \(\frac{3}{x}+\frac{y}{7}-\frac{xy}{8}+9\)	4	\(\frac{3}{x},\frac{y}{7},-\frac{xy}{8},9\text{ }\And \text{ }so\text{ }on\)

Factors:
When two or more numbers are multiplied together, the numbers themselves are called the factors of the product. The factors of 34 are 2 and 17. The factors of 18x² are 2, 3 and x, factors of ln are l and n (8 is numerical factor of 8x and x is variable factor of 8x)

Coefficient:
Any factor of a product is the coefficient of the remaining factors. In the product of 8 × 5, the number 8 is coefficient of 5 and 5 is coefficient of 8. In the product 5yz, 5 is the (numerical) coefficient of yz, 5y is the coefficient of z and 5z is coefficient of y and yz is the variable coefficient of 5.
Note : If a letter has no coefficient written before it, the coefficient 1 is understood. Thus y means 1y and yz means 1yz, similarly, –y means –1(y).

Terms

An algebraic expression is a combination of numbers, literals and arithmetical operations. One or more sings (+ and –) separates an expression into several parts. Each part along with its sign is called a term.

Type of Algebraic Expression	Definition	Examples
1. Monomial	A monomial is an expression having one term.	6, –5xy, –6x² etc.
2. Binomial	A binomial is an algebraic expression having two terms.	2x – 3y, x – y, 3x² – 6x, (x – y)² + 3xy, 3x² + 5 etc.
3. Trinomial	A trinomial is an algebraic expression having three terms.	2a – 3b – 5c, 5y² – 3x + 9, a³ + b³ + c³ etc.
4.Tetranomial or Quadrinomial	A quadrinomial is an algebraic expression having four terms.	a + b + c – 3, a³ + b³ + c³ + 3abc, etc.
5. Polynomial	Binomial, trinomials and all algebraic expressions having more than three terms are called polynomials.	2a – 3b, x + y – 3yz + 4x² – 6y² etc.

Note :
(i) The words ‘mono’, ‘bi’, ‘tri’ and ‘poly’ mean one, two, three and many.
(ii) A term of an algebraic expression having no literal factor is called a constant term, for example, in x² + 9x – 8, the constant term is –8.

Example 1: Classify the following algebraic expressions into monomial, binomial, and trinomial:
a + b, 4x + 3y – 7z, y², 1 + x + x², z² + 2
Solution: Monomial: y²
Binomials: a + b, z² + 2
Trinomials: 4x + 3y – 7z, 1 + x + x²

Example 2: Find the value of a² + x², if a = 2 and x = 3.
Solution: a² + x² = a × a + x × x
= 2x²+ 3x³
= 4 + 9 = 13

Example 3: Write an algebraic expression whose terms are
(a) 7, 4x, 3xy (b) 4xy², 3x²y, -9
Solution:
(a) The algebraic expression with terms
7, 4x, and 3xy = 7 + 4x + 3xy
(b) The algebraic expression with terms
4xy², 3x²y, and – 9 = 4xy² + 3x²y + (- 9)
= 4xy² + 3x²y – 9

Like (Similar) and Unlike (Dissimilar ) Terms

These terms are defined as follows:

Like (Similar terms)	Unlike (Dissimilar terms)
These are terms whose literal (variable) factors are the same. For example, (i) 5x², – 6x², + 3x²(ii) 2(a + b), – 4(a + b), 6(a + b) (iii) 6xy², –8xy², xy²	These are terms whose literal (variable) factors are not same. For example, (i) 2x and 5y (ii) 6xy² and 8x²y (iii) (x + y), (x² + y), 5(x² + y²)

Finding the Value of an Algebraic Expression

An algebraic expression contains literal (variable) numbers. If we know the numerical values of these variables and substitute them in the given algebraic expression we get a numerical expression which can be simplified by the methods of arithmetic to get a number, called the value of the algebraic expression.

Eg: Evaluate the following expression if a = 2, b = – 1, c = 1: a² + b²+ c² – ab – bc – ca.
Solution:
a² + b² + c² – ab – bc – ca
= (2)² + (–1)² + (1)² – 2 × (–1) – (–1) × 1 – 1 × 2
= 4 + 1 + 1 + 2 + 1 – 2
= 9 – 2 = 7
So, a² + b² + c² – ab – bc – ca at a = 2, b = – 1, c = 1 has value 7.

Addition and Subtraction of Algebraic Expressions

Like Terms :

The sum of two or more like terms is a like term with a numerical coefficient equal to the sum of the numerical coefficients of all the like terms.
The difference between two like terms is a like term with a numerical coefficient equal to the difference between the numerical coefficients of the two like terms.

Addition and Subtraction of Algebraic Expressions Problems with Solutions

1. Add 2x², 5x² and x².
Solution:
The three like terms are 2x², 5x² and x²
Adding these terms, we have 2x² + 5x² + x²
= (2 + 5 + 1) x²(Distributive property)
= 8x²

2. Add – xy, –5xy, –2xy.
Solution:
Adding the given three like terms, we have
= – xy + (– 5xy) + (– 2xy) = –xy –5xy – 2xy
= (–1 – 5 – 2) xy = – 8xy

3. Add –7x, –5x, 8x, 9x.
Solution:
Positive terms are 8x, 9x
Negative terms are – 7x, – 5x
Sum of positive terms = 8x + 9x = 17x
Sum of negative terms = – 7x + (–5x)
= – 7x – 5x = – 12x
Adding these two terms, we have
17x + (–12)x = 17x – 12x = (17 – 12)x = 5x

4. Add 4x + 3y – 5z, –7z + 5x – 8y and – y –3x + 2z.
Solution:
Column method:
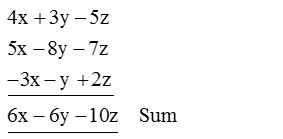
Algebraic Expression 1
Re-write the expressions so that their like terms are in a column as
Horizontal Method :
Sum = (4x + 3y – 5z) + (–7z + 5x – 8y) + (–y –3x + 2z)
= 4x + 3y – 5z –7z + 5x – 8y – y –3x + 2z
= (4x + 5x –3x) + (3y – 8y – y) + ( – 5z – 7z +2z)
= (4 + 5 – 3) x + (3 – 8 – 1) y + (–5 –7 + 2)z
= 6x – 6y –10z

5. Subtract 10x² from –8x².
Solution:
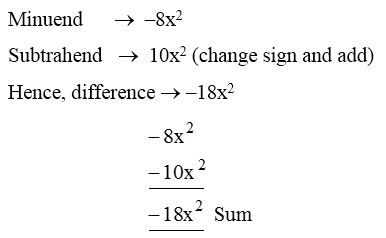
Algebraic Expression 2

6. How much is t² – 5t + 6 greater than t² + 5t – 6 ?
Solution:
Algebraic Expression 3

Rule for Solving Algebraic Expressions

BODMAS represents the order of Performance of operations namely BODMAS represents the order of Performance of operations namely
B = Brackets;
O = Of;
D = Division;
M = Multiplication;
A = Addition;
S = Subtraction

Examples:

1. Simplify : 2x – [3y – {2x – (y – x)}].
Solution:
We have, 2x – [3y – {2x – (y – x)}]
We first remove the inner most bracket.
2x – [3y – {2x – y + x}]
Next inner most is the curly bracket.
2x – [3y – 2x + y – x]
Now we remove the square bracket.
2x – 3y + 2x – y + x
= (2x + 2x + x) – 3y – y
= (2x + 2x + x) – (3y + y)
= (2 + 2 + 1) x – (3 + 1) y = 5x – 4y

2. Simplify : 5a – [a² – {2a (1 – a + 4a²) –3a (a² – 5a – 3)}] – 8a.
Solution:
We first remove the inner most grouping symbol ( ), the { } and then [ ].
Thus we have,
5a – [a² – {2a (1 – a + 4a²) –3a (a² – 5a – 3)}] – 8a
= 5a –[a² –{2a –2a² + 8a³ – 3a³ + 15a² + 9a}] – 8a
= 5a –[a² – 2a + 2a² – 8a³ + 3a³ – 15a² – 9a] – 8a
= 5a – a² + 2a – 2a² + 8a³ – 3a³ + 15a² + 9a – 8a
= 5a³ + 12a² + 8a.