Adding and Subtracting Fractions
To ADD and/or SUBTRACT ALGEBRAIC FRACTIONS:
In order to add or subtract (or “combine”), algebraic fractions, a common denominator is needed. (This is the same process you use when adding and subtracting “regular number fractions”).
Numerical Denominators:
- First, choose the least common denominator (lcd). This is the smallest number that all denominators can divide into.

- If any denominator in the problem is already the lcd, the numerator of that fraction stays the same (because the adjustment would be a multiplication times 1). If any denominator in the problem is not the lcd, multiply that numerator and denominator by the same value that was needed to create the lcd.

- Combine the problem into one fraction:
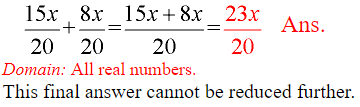
- Combine like terms in the numerator and reduce the resulting fraction (if needed).
This same process applies when the denominators contain a variable.
Variable Denominators:
- When one or more of the denominators contains a variable, the same process (described above) is used. When the denominator contains a variable, the LCD will need to contain the largest power of that variable present. Start by finding the LCD.
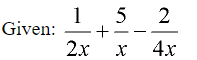
The Least Common Denominator (LCD) is 4x.
The largest power of x in this problem is 1, so the LCD contains x to the first power, multiplied by the common denominator for 2 and 4 (which is 4). Domain: x ≠0 - Adjust each fraction to contain the LCD. Be sure to adjust the numerator by the SAME value used to adjust its denominator.
Multiply each denominator (and its corresponding numerator) by a value what will create the LCD of 4x.
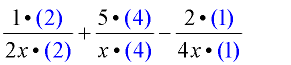
It is not necessary to show the multiplication by (1). - Combine the problem into one fraction. Combine any similar terms in the numerator.
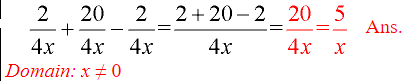
This final answer was then reduced further.
Example 1: (Use of parentheses.)
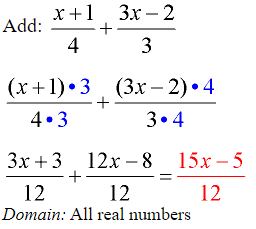
The LCD in this problem is 12.
When adjusting for the LCD, it is necessary to multiply BOTH the numerator and denominator in each fraction by the numerical values of 3, and then 4.
Example 2: (Subtracting a quantity.)
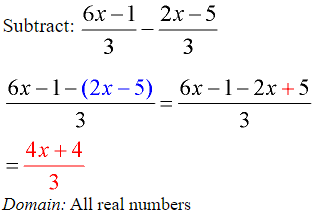
At first glance, this problem looks easy because it already has a common denominator.
A potential “problem spot” in this example is the subtraction of the second numerator. You must subtract the ENTIRE second numerator, not just the first term. Use parentheses around the numerator being subtracted!! When you distribute the negative sign across the parentheses you will be subtracting both terms in the second numerator.
Example 3: (Variable denominators.)
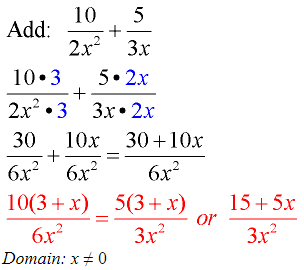
The LCD in this problem is 6x².
The largest power of x is 2 and the common denominator for 2 and 3 is 6.
Be careful to combine only “like” terms (30 and 10x are not “like” terms).
When finished, look for common factors in the numerator to see if the answer can be reduced further. This fraction can be reduced further.
